陳述
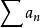 達朗貝爾判別法
達朗貝爾判別法 達朗貝爾判別法
達朗貝爾判別法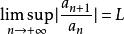 達朗貝爾判別法
達朗貝爾判別法設為無窮級數,其中每一項都是不為0的實數或複數,如果(裡面的項為複數時就是取模),則
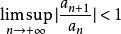 達朗貝爾判別法
達朗貝爾判別法若,級數絕對收斂。(裡面的項為複數時就是取模)
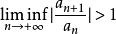 達朗貝爾判別法
達朗貝爾判別法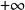 達朗貝爾判別法
達朗貝爾判別法若(包括發散到的情況),級數發散。
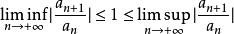 達朗貝爾判別法
達朗貝爾判別法若非以上兩者, 即時,級數可能收斂也可能發散。
證明
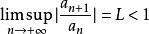 達朗貝爾判別法
達朗貝爾判別法 達朗貝爾判別法
達朗貝爾判別法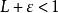 達朗貝爾判別法
達朗貝爾判別法 達朗貝爾判別法
達朗貝爾判別法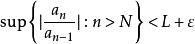 達朗貝爾判別法
達朗貝爾判別法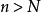 達朗貝爾判別法
達朗貝爾判別法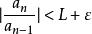 達朗貝爾判別法
達朗貝爾判別法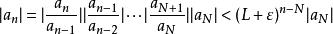 達朗貝爾判別法
達朗貝爾判別法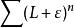 達朗貝爾判別法
達朗貝爾判別法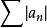 達朗貝爾判別法
達朗貝爾判別法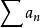 達朗貝爾判別法
達朗貝爾判別法設。選取使得。對充分大的,有。所以時,有。然後,。考慮,這是一個公比在0與1之間的無窮等比級數,所以收斂。由比較審斂法,知收斂,即絕對收斂。
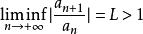 達朗貝爾判別法
達朗貝爾判別法 達朗貝爾判別法
達朗貝爾判別法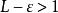 達朗貝爾判別法
達朗貝爾判別法 達朗貝爾判別法
達朗貝爾判別法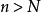 達朗貝爾判別法
達朗貝爾判別法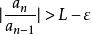 達朗貝爾判別法
達朗貝爾判別法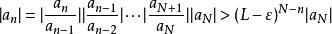 達朗貝爾判別法
達朗貝爾判別法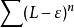 達朗貝爾判別法
達朗貝爾判別法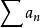 達朗貝爾判別法
達朗貝爾判別法若,則選取使得。對充分大的,時,有。然後,。考慮,其公比大於1,故發散。由比較審斂法,知發散。
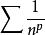 達朗貝爾判別法
達朗貝爾判別法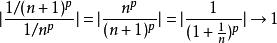 達朗貝爾判別法
達朗貝爾判別法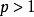 達朗貝爾判別法
達朗貝爾判別法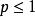 達朗貝爾判別法
達朗貝爾判別法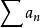 達朗貝爾判別法
達朗貝爾判別法最後,考慮p級數,。又因為p級數當時收斂,時發散,所以可能收斂也可能發散。
