陳述
 根值審斂法
根值審斂法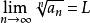 根值審斂法
根值審斂法 根值審斂法
根值審斂法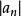 根值審斂法
根值審斂法設為一無窮級數,如果,(這裡也可以是複數,此時代表複數的模),則
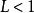 根值審斂法
根值審斂法時級數絕對收斂;
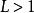 根值審斂法
根值審斂法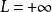 根值審斂法
根值審斂法(包括) 時級數發散;
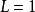 根值審斂法
根值審斂法時級數可能收斂也可能發散。
證明
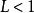 根值審斂法
根值審斂法 根值審斂法
根值審斂法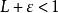 根值審斂法
根值審斂法 根值審斂法
根值審斂法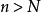 根值審斂法
根值審斂法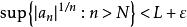 根值審斂法
根值審斂法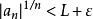 根值審斂法
根值審斂法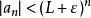 根值審斂法
根值審斂法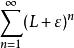 根值審斂法
根值審斂法 根值審斂法
根值審斂法設,選取使得。對充分大的,時有,從而,。因為是無窮等比級數,所以收斂。由比較審斂法,知收斂。
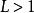 根值審斂法
根值審斂法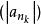 根值審斂法
根值審斂法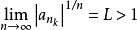 根值審斂法
根值審斂法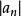 根值審斂法
根值審斂法 根值審斂法
根值審斂法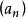 根值審斂法
根值審斂法 根值審斂法
根值審斂法若,則有一收斂子數列,。於是有無限多個的項大於1。但若要收斂,則數列的極限必須為0。因此,發散。
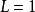 根值審斂法
根值審斂法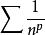 根值審斂法
根值審斂法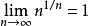 根值審斂法
根值審斂法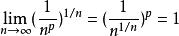 根值審斂法
根值審斂法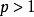 根值審斂法
根值審斂法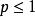 根值審斂法
根值審斂法 根值審斂法
根值審斂法若,以p級數為例,因為,所以,又因為p級數當時收斂,時發散,所以可能收斂也可能發散。

