概念
 稜錐
稜錐2.稜錐的兩個特徵稜錐是多面體中重要的一種,它有兩個本質特徵:①有一個面是多邊形;②其餘的各面是有一個公共頂點的三角形,二者缺一不可。因此稜錐有一個面是多邊形,其餘各面都是三角形。但是也要注意“有一個面是多邊形,其餘各面都是三角形”的幾何體未必是稜錐。
3.稜錐的分類稜錐的底面可以是三角形、四邊形、五邊形……我們把這樣的稜錐分別叫做三稜錐、四稜錐、五稜錐。
4.正稜錐如果一個稜錐的底面是正多邊形,並且頂點在底面的射影是底面的中心,這樣的稜錐叫做正稜錐。如圖,若稜錐P-AC的底面是正多邊形,且PO底面AC,O為垂足,O是正多邊形的中心,則稜錐P-AC是正稜錐。(如圖) 正稜錐的斜高:正稜錐側面等腰三角形底邊上的高,叫做正稜錐的斜高。性質
1.稜錐截面性質定理及推論
定理:如果稜錐被平行於底面的平面所截,那么所得的截面與底面相似,截面面積與底面面積的比等於頂點到截面距離與稜錐高的平方比。
推論1:如果稜錐被平行與底面的平面所截,則稜錐的側棱和高被截面分成的線段比相等。
推論2:如果稜錐被平行於底面的平面所截,則截得的小稜錐與已知原稜錐的側面積之比也等於它們對應高的平方比;截得的稜錐與已知稜錐的側面積之比也等於它們的底面積之比。
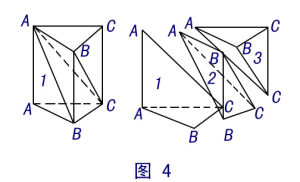
2.一些特殊稜錐的性質側棱長都相等的稜錐,它的頂點在底面內的射影是底面多邊形的外接圓的圓心(外心),同時側棱與底面所成的角都相等。側面與底面的交角都相等的稜錐,它的二面角都是銳二面角,所以頂點在底面內的射影在底多邊形的內部,並且它到各邊的距離相等即為底多邊形的內切圓的圓心(內心),且各側面上的斜高相等。如果側面與底面所成角為α,則有S底=S側cosα。如圖畫出了射影是外心和內心的情況。
3.稜錐的側面積及全面積、體積公式稜錐的側面積及全面積稜錐的側面展開圖是由各個側面組成的,展開圖的面積,就是稜錐的側面積,則S稜錐側=S1+S2+…+Sn(其中Si,i=1,2…n為第i個側面的面積)S全=S稜錐側+S底稜錐的體積 稜錐和圓錐統稱錐體,錐體的體積公式是: (s為錐體的底面積,h為錐體的高)。
4.正稜錐有下面一些性質正稜錐各側棱相等,各側面都是全等的等腰三角形,各等腰三角形底邊上的高相等(它叫做正稜錐的斜高);正稜錐的高、斜高和斜高在底面內的射影組成一個直角三角形,正稜錐的高、側棱、側棱在底面內的射影也組成一個直角三角形。正稜錐的側棱與底面所成的角都相等;正稜錐的側面與底面所成的二面角都相等。正稜錐的側面積:如果正稜錐的底面周長為c,斜高為h’,那么它的側面積是 s=1/2ch
直觀圖畫法
正稜錐的直觀圖由底面和頂點所決定。正稜錐底面的畫法與直稜柱底面的畫法相同。頂點和底面中心的距離等於它的高。下面以正五稜錐為例,說明正稜錐的直觀圖的畫法。畫一個底面邊長為5 cm,高為11.5 cm的正五稜錐的直觀圖,比例尺是 。
畫法:
(1)畫軸。畫x′軸、y′軸、z′軸,記坐標原點為O′,使∠x′O′y′=45°(或135°),∠x′O′z′=90°。如圖(1)
 稜錐
稜錐(2)畫底面。按x′軸、y′軸畫正五邊形的直觀圖ABCDE,按比例尺取邊長等於5÷5=1(cm),並使正五邊形的中心對應於點O′。
(3)畫高線。在z′軸取O′S=11.5÷5=2.3(cm)。
(4)成圖。連結SA、SB、SC、SD、SE,並加以整理(去掉輔助線,將被遮擋的部分改為虛線),就得到所畫的正五稜錐的直觀圖。
定義
稜錐的底面和平行於底面的一個截面間的部分,叫做稜台。由三稜錐,四稜錐,五稜錐……截得的稜台,分別叫做三稜台,四稜台,五稜台。
由正稜錐截得的稜台叫做正稜台。
性質
正稜台的性質:
(1)正稜台的側棱相等,側面是全等的等腰梯形。各等腰梯形的高相等,它叫做正稜台的斜高;
四稜台
四稜台
(2)正稜台的兩底面以及平行於底面的截面是相似正多邊形;
(3)正稜台的兩底面中心連線、相應的邊心距和斜高組成一個直角梯形;兩底面中心連線、側棱和兩底面相應的半徑也組成一個直角梯形。
相關名稱
兩個平行的面分別叫做上底面和下底面,其餘的面叫做側面,側面相交的線段叫做側棱,3條側棱相交的點叫做頂點。
正稜台各側面的高叫做稜台的斜高。
體積公式
稜台的體積公式:V=[S+S'+(SS')^(1/2)]h/3