正則配分函式
正文
正則系綜的重要數量,它決定了在正則系綜的最可幾分布中,能量在體系間的分配方式。正則配分函式Q可用下式表示: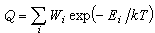
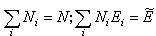 的條件下(式中 Ni為具有Ei的體系數,愛為系綜的總能量;N為體系總數),利用機率論和拉氏未定乘因子法可以得出,在最可幾分配方式中,能量為Ei的體系在系綜中出現的幾率Pi為:
的條件下(式中 Ni為具有Ei的體系數,愛為系綜的總能量;N為體系總數),利用機率論和拉氏未定乘因子法可以得出,在最可幾分配方式中,能量為Ei的體系在系綜中出現的幾率Pi為: 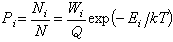
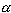 、平均能量唕、平均熵宑為:
、平均能量唕、平均熵宑為: 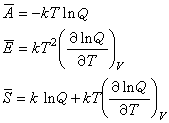
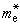
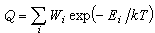
正則系綜的重要數量,它決定了在正則系綜的最可幾分布中,能量在體系間的分配方式。
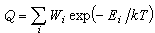
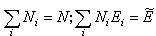 的條件下(式中 Ni為具有Ei的體系數,愛為系綜的總能量;N為體系總數),利用機率論和拉氏未定乘因子法可以得出,在最可幾分配方式中,能量為Ei的體系在系綜中出現的幾率Pi為:
的條件下(式中 Ni為具有Ei的體系數,愛為系綜的總能量;N為體系總數),利用機率論和拉氏未定乘因子法可以得出,在最可幾分配方式中,能量為Ei的體系在系綜中出現的幾率Pi為: 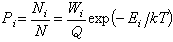
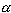 、平均能量唕、平均熵宑為:
、平均能量唕、平均熵宑為: 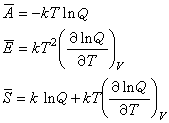
巨正則配分函式(英語:Partition function)是一個平衡態統計物理學中經常套用到的概念,經由計算配分函式可以將微觀物理狀態與巨觀物理量相互...
巨正則配分函式 配圖 相關連線統計系綜3.1 正則系綜3.1.1 正則系綜與正則配分函式3.1.2 正則配分函式與熱力學量的關係3.1.3 正則配分函式在經典統計力學相空間中的形式3.2 巨正則系綜3.2.1 巨正則系綜和巨正則配分函式3.2.2...
內容簡介 作者簡介 圖書目錄正則配分函式 16獨立離域於體系的正則配分函式 17巨正則系綜 18巨正則系綜和熱力學 19巨正則配分函式 110微正則系綜... 第四章非理想氣體 41非理想氣體的正則配分函式及構型積分 42非...
正則系綜和正則配分函式27-2 正則配分函式和熱力學函式27...
內容介紹 本書目錄正則系綜 27-1 正則系綜和正則配分函式 27-2 正則配分函式和...
圖書信息 內容簡介 目錄正則系綜和正則配分函式104 實際氣體及其統計處理105 1實際氣體的正則配分函式105 構型積分及其簡化處理法108 用於...
基本信息 目錄的簇展開表示巨正則配分函式能展開為單體(理想氣體)、兩體、多體(簇...
由來 推導 表示性質,首先就要尋求溶液的正則配分函式。按似晶模型,關鍵仍在如何清點被安置...
概述 理論基礎 似晶格模型 套用 不足