微觀狀態數

概述

體系中所有與巨觀狀態相容的量子態的總數。處在一定已知巨觀約束下的體系的平衡態，可用一組獨立的巨觀參量描述。這一組巨觀參量的特定數值確定一個巨觀狀態。例如，孤立是一種約束，對全國粒子體系，其巨觀狀態可用總粒子數N、能量E、體積 V描述。體系只能處在與巨觀狀態相容的那些量子態上，這樣的量子態稱為體系的可及微觀狀態，其總數目稱為體系的可及微觀狀態數，用Ω 表示。

獨立子體系的Ω 可通過能級分布進行求算。考慮全同粒子組成的孤立體系時，其巨觀狀態用N、E、 V描述。令εi(i=1,2,3,…)為單粒子的可及微觀狀態的能量，它的簡併度為ωi，能量為εi的各狀態上的粒子數為ni,它們必須同時滿足下列守恆條件：

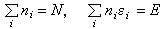
n1,n2,…,ni,…稱為與巨觀狀態(N,E,V)相容的能級分布。一個巨觀狀態可有很多種能級分布，而每種能級分布又擁有大量的微觀狀態。所有能級分布中微觀狀態數最多的分布稱為最可幾分布，當N→∞時,最可幾分布所擁有的微觀狀態數趨於體系的可及微觀狀態數Ω ：

式中ni是能級εi上最可幾分布的粒子數，它服從麥克斯韋－玻耳茲曼分布律。

觀狀態數與相對分子質量

熵值可以看作是體系微觀狀態數的函式。相對分子量越大，可能的微觀狀態數也越大。比如核外電子的可能排布，核內粒子的自鏇狀態等。原子核也有自鏇啊。自鏇只是一種量子現象，並沒有現實狀態和它對應。比如F的自鏇量子數為1/2，Cl的自鏇量子數為3/2。複雜分子的微觀狀態數也大於簡單分子。比如乙烷可以有交叉和重疊兩種構像，而甲烷沒有。對稱性高的分子顯然微觀狀態數比較少，因為許多狀態通過對稱變換都是一樣的。甲醚是中心對稱分子，熵值自然敵一些。