由來
許多實驗表明,氣體的性質都在不同程度上偏離玻意耳-馬略特定律,壓強越低,這種偏離越小,只有當壓強趨近於零的極限情形下,玻意耳-馬略特定律才是完全正確的。這種氣體稱為理想氣體。一般情況下,實際氣體的性質接近理想氣體,而在壓強趨於零時完全變為理想氣體。
為了描述實際氣體,H.開默林-昂內斯於1901年把一摩爾的實際氣體狀態方程表示成
pV=A+Bp+Cp +Dp +……
或
pV=A+B'/V+C'/V +D'/V +……
上述A、B、C、D、…或A、B'、C'、D'、…就分別稱為第一、第二、第三、第四、……維里係數,它們都是溫度的函式。當壓強趨於零(或體積趨於無窮大)時,A=RT(R是摩爾氣體常數),於是上面兩式就變成玻意耳-馬略特定律。各個維里係數都可由實驗測定。實驗表明,維里係數A、B、C、D、…或A、B'、C'、D'、…依次減小得很快,在實際套用上只需前兩、三項就夠了。
統計物理學認為,實際氣體對理想氣體的偏離是由於粒子之間的相互作用引起的。套用統計方法可以研究非理想氣體的性質。先把巨配分函式的對數展成級數,再根據它同壓強、溫度和體積的關係即可求得級數形式的實際氣體物態方程。這種方法適合於溫度不太低或密度不太高的系統,也就是說適用於對理想氣體稍有偏離的氣體系統,並只考慮粒子間的二體相互作用。由此可以得到壓強p按比容的倒數1/v的維里展開這就是實際氣體的狀態方程式,是壓強按粒子數密度(即1/υ)的冪級數展開式。式中b、-b、4b-2b、為第一、第二、第三、第四、……維里係數,它們是同集團積分bι(V,T)(l=1,2,3,…集團中的點數)在V趨於無窮大時的極限值b、b、b、b、…相聯繫的(見集團展開)。
推導
得到維里係數解析式的第一步是根據巨正則系綜配分函式的簇展開(Cluster expansion):
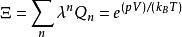 維里係數
維里係數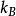 維里係數
維里係數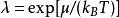 維里係數
維里係數 維里係數
維里係數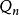 維里係數
維里係數其中,p是壓強,V是系統體積, 是波茲曼常數,T是絕對溫度, 是逸度, 是化學勢。 為包含n個粒子的子系統的配分函式:
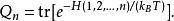 維里係數
維里係數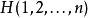 維里係數
維里係數其中, 是包含n個粒子子系統的哈密頓量,為粒子動能與勢能之和。勢能相不僅包含兩體作用,也包括了三體和多體的作用。
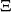 維里係數
維里係數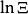 維里係數
維里係數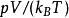 維里係數
維里係數的簇展開表示巨正則配分函式能展開為單體(理想氣體)、兩體、多體(簇)相互作用的貢獻之和。根據定義, 等於 ,與維里展開
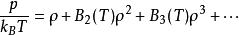 維里係數
維里係數相比較,可得
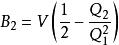 維里係數
維里係數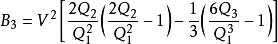 維里係數
維里係數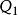 維里係數
維里係數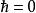 維里係數
維里係數等等。此為內含動能項的量子統計表達式。注意到 僅僅包括動能項;熱力學極限下 ,動能算符和勢能算符可對易,分子與分母的動能項互相消去。求解矩陣的跡成為對構型空間的積分,結果是經典的維里係數只由粒子間相互作用決定,而相互作用只由粒子坐標決定。因此可通過對構型空間積分求算維里係數。
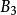 維里係數
維里係數然而,比 更高階的維里係數的遞推式變得非常複雜。約瑟夫·愛德華·邁耶和瑪麗亞·格佩特-梅耶提出了圖形表記積分式的方法演算維里係數。
他們引入了被稱為邁耶函式的表達式:
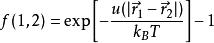 維里係數
維里係數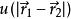 維里係數
維里係數物理上表示玻爾茲曼因子與理想氣體的偏差。並將簇展開整理成邁耶函式的組合。此處 表示粒子1與2(假設所有粒子全同)間的勢能。
表示
邁耶函式表示的維里係數
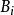 維里係數
維里係數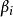 維里係數
維里係數維里係數 與不可約的邁耶簇積分 通過下式相關聯:
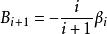 維里係數
維里係數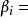 維里係數
維里係數而 不可約的邁耶圖中黑色與白色節點間的邊對應的邁耶函式之乘積的積分之和。
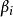 維里係數
維里係數從邁耶圖得 積分式的規則為:
(1)構造一個有i個頂點的圖,並給頂點編號為k=1,..,i,對應一個含有大小為i的簇中各個粒子。
(2)將編號為0的粒子坐標設為原點,標記為白色,其它頂點標記為黑色。
(3)將圖的每個邊則與邁耶函式關聯,其自變數為這兩個頂點所對應的粒子的距離。
(4)進行構型空間下的積分。
(5)將結果乘上當前圖的對稱階數,其數值等於改變黑色粒子編號但圖在拓撲上仍然等同的排列數目。
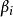 維里係數
維里係數(6) 等於所有重複前述步驟構造不同拓撲結構的不可約邁耶圖對應的積分之和。
於是第二維里係數的表達式是
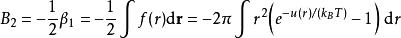 維里係數
維里係數第三維里係數的表達式是
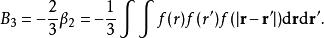 維里係數
維里係數
