系綜
在統計物理中, 系綜(英語: ensemble)代表一定條件下一個體系的大量可能狀態的集合。也就是說,系綜是系統狀態的一個機率分布。對一相同性質的體系,其微觀狀態(比如每個粒子的位置和速度)仍然可以大不相同。(實際上,對於一個巨觀體系,所有可能的微觀狀態數是天文數字。)在機率論和數理統計的文獻中,使用“機率空間”指代相同的概念。
統計物理的一個原理(各態歷經原理)是:對於一個處於平衡的體系,物理量的時間平均,等於對對應系綜里所有體系進行平均的結果。
體系的平衡態的物理性質可以對不同的微觀狀態求和來得到。系綜的概念是由約西亞·吉布斯在1878年提出的。
常用的系綜有:
•微正則系綜(microcanonical ensemble):系綜里的每個體系具同的能量(通常每個體系的粒子數和體積也是相同的)。
•正則系綜(canonical ensemble):系綜里的各體系可以和其他體系交換能量(每個體系的粒子數和體積仍然是固定且相同的),但系綜內各體系有相同的溫度。
•巨正則系綜(grand canonical ensemble):正則系綜的推廣,各體系可以和其他體系交換能量和粒子,但系綜內各個體系有相同的溫度和化學勢。
•等溫等壓系綜(isothermal-isobaric ensemble):正則系綜的推廣,各體系可以和其他體系交換能量和體積,但系綜內各個體系有相同的溫度和壓強。
在系綜中,物理量的變化範圍(fluctuation)與其本身大小的比值會隨著體系變大而減小。於是,對於一個巨觀體系,從各種系綜計算出的物理量的差異將趨向於零。
目錄
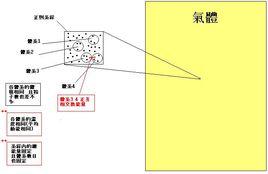
正則系綜( canonical ensemble)是統計力學中系綜的一種。它代表了許多具有相同溫度的體系的集合。正則系綜是最普遍套用的系綜。
 正則系綜
正則系綜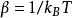 正則系綜
正則系綜 正則系綜
正則系綜 正則系綜
正則系綜正則系綜內每個體系的粒子數和體積都是固定的。但每個體系都可以和系綜內其他體系交換能量。同時系綜里所有體系的能量總和,以及體系的個數是固定的。在這些條件下,當系綜內所有體系被分配到不同的微觀態上,我們發現:處於每個微觀態的體系的個數正比於。其中,是玻爾茲曼常數,是絕對溫度。
 正則系綜
正則系綜正則系綜的配分函式,,是:
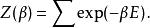 正則系綜
正則系綜 正則系綜
正則系綜配分函式的對數就是亥姆霍茲自由能(Helmholtz free energy,符號)
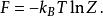 正則系綜
正則系綜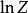 正則系綜
正則系綜 正則系綜
正則系綜當分函式計算出以後,平均能量可以直接從對一階導數中求得。
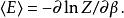 正則系綜
正則系綜參考
•統計物理
•微正則系綜
•巨正則系綜
•等溫等壓系綜