正三稜柱:正三稜柱是上下底面是全等的兩正三角形，側面是矩形，側棱平行且相 -百科知識中文網

正三稜柱是上下底面是全等的兩正三角形，側面是矩形，側棱平行且相等的稜柱，並且上下底面的中心連線與底面垂直，也就是側面與底面垂直。（正三稜柱含於直三稜柱，即正三稜柱是底面是正三角形的直三稜柱）

正三稜柱不一定有內切球：若正三稜柱有內切球,則正三稜柱的高一定是球的直徑，此時正三稜柱的棱長為底面邊長的(根號3)/3倍；

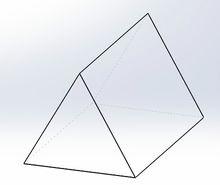正三稜柱一定有外接球：但直徑一定不是正三稜柱的高，直徑為根號(h^2+4a^2/3),其中h為三稜柱的高,a為底面邊長。

附註：正三稜柱的外接球半徑求解過程

令上下的等邊三角形邊長為a，側棱長為h

由等邊三角形的性質，容易證明三角形幾何中心到三角形三頂點的距離：S = （√3）/3

現在想像用一把刀從三稜柱的中間水平切割過去，把三稜柱切成了兩個相同的三稜柱

那么新出現的平面的中心到原三稜柱的距離均為√[（h^2）+4*（a^2）/3]{勾股定理}

那么這個點就是外接球心這個共同距離就是半徑

體積為：V=SH

正三棱塊

當正三稜柱的側面是正方形時，該正三稜柱即正三棱塊，如下圖示。

正三稜柱