定義
 三稜柱
三稜柱兩底面互相平行,側面都是四邊形,並且每相鄰兩個四邊形的公共邊都互相平行,由這些面所圍成的幾何體叫做稜柱,兩個互相平行的面叫做稜柱的底面,其餘各面叫做稜柱的側面,兩個側面的公共邊叫做稜柱的側棱,側面與底面的公共頂點叫做稜柱的頂點,不在同一個面上的兩個頂點的連線叫做稜柱的對角線,兩個底面的距離叫做稜柱的高。
底面是三角形、四邊形、……的稜柱分別叫做三稜柱、四稜柱、……
稜柱的性質
稜柱具有以下幾個性質:
(1)側棱都相等,側面是平行四邊形;
(2)兩個底面與平行於底面的截面是全等的多邊形;
(3)過不相鄰的兩條側棱的截面是平行四邊形;
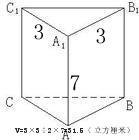 三稜柱
三稜柱(4)橫截面積和長度一定時,三稜柱狀物體縱向支持力最大,橫向承受力最小(橫向受力使物體產生拉應力,縱向產生壓應力.理論上壓應力對物體有增強作用,拉應力著相反);
(5)稜柱體積=底面積×高。
稜柱分類
稜柱:一般的,有兩個面相互平行,其餘各面都是四邊形,並且相鄰兩個側面的交線相互平行的多面體叫做稜柱。
直三稜柱:是各個側面的高相等,底面是三角形,上表面和下表面平行且全等,所有的側棱相等且相互平行且垂直於兩底面的稜柱。上下表面三角形可以是任意三角形。正三稜柱是直三稜柱的特殊情況,即上下面是正三角形。
正三稜柱:三條側棱皆平行,上表面和下表面是平行且全等的正三角形。正稜柱是側棱都垂直於底面,且底面是正多邊形的稜柱。
特別注意:底面為正多邊形,側棱垂直於底面,但是側棱和底面邊長不一定相等。
所以說,直三稜柱是很特殊的稜柱,正因為特殊所以是數學上性質比較好研究的。類似於正方形是最特殊的四邊形一樣。右邊的圖非常直觀,就是高中數學課本上最常見的直三稜柱。