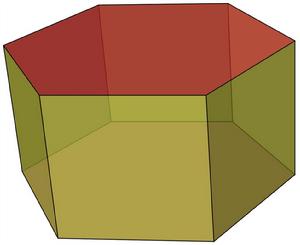
稜柱
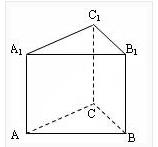圖1.正三稜柱稜柱是幾何學中的一種常見的三維多面體，指兩個平行的平面被三個或以上的平面所垂直截得的封閉幾何體。
若用於截平行平面的平面數為n，那么該稜柱便稱為n-稜柱。如三稜柱就是由兩個平行的平面被三個平面所垂直截得的封閉幾何體。
稜柱的各種屬性
底面
稜柱中兩個互相平行的面，叫做稜柱的底面與側面垂直。
側面
稜柱中除兩個底面以外的其餘各個面都叫做稜柱的側面。
側棱
稜柱中兩個側面的公共邊叫做稜柱側棱。
頂點
稜柱中側面與底面的公共頂點叫做稜柱的頂點。
對角線
稜柱中不在同一平面上的兩個頂點的連線叫做稜柱的對角線。
高
稜柱的兩個底面的距離叫做稜柱的高。
對角面
稜柱中過不相鄰的兩條側棱的截面叫做稜柱的對角面。
體積
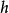正稜柱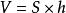
正稜柱
正稜柱假設一個稜柱的底面面積為，高為，那么這個稜柱的體積為：。
一些特殊的稜柱
斜稜柱
側棱不垂直於底面的稜柱叫做斜稜柱，畫斜稜柱時，一般將側棱畫成不與底面垂直。
直稜柱
側棱垂直於底面的稜柱叫做直稜柱。畫直稜柱時，應將側棱畫成與底面垂直。
正稜柱
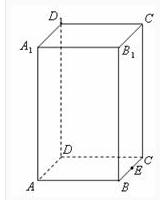圖2.正四稜柱底面是正多邊形的直稜柱叫做正稜柱。正稜柱是側棱都垂直於底面，且底面是正多邊形的稜柱。特別注意：底面為正多邊形，側棱垂直於底面，但是側棱和底面邊長不一定相等。而直稜柱側棱也是垂直於底面，側棱和底面邊長不一定相等，而且底面多邊形形狀也不確定。
正稜柱性質
(1)正稜柱的側棱垂直於底面。
(2)正稜柱的側面與底面相互垂直。
(3)正稜柱的側面為矩形，但不一定是正方形。
