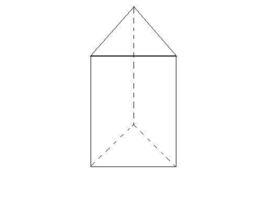
簡單介紹
直稜柱的上下底面可以是三角形、四邊形、五邊形、六邊形等多邊形，側面都是長方形（含正方形）。根據底面圖形的邊數，我們稱它為直三稜柱、直四稜柱（長方體和立方體都是直四稜柱）、直五稜柱、直六稜柱 。它們如圖1所示：
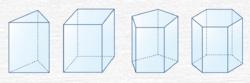圖1直三稜柱、直四稜柱、直五稜柱、直六稜柱其中“棱”是指兩個面的公共邊，它具有以下特徵：
（1）有兩個面互相平行，稱它們為底面；
（2）其餘各個面均為矩形，稱它們為側面；
（3）側棱（指兩個側面的公共邊）垂直於地面。
性質
1.側棱與底面垂直；
2.側棱長（最長的一條）與高相等；
3.側面與對角面都是矩形；
4.側面展開圖是矩形；
5.側面積=底面周長×側棱長；
6.體積=底面積×側棱長；
7.表面積=側面積+兩個底面積；
8.直稜柱相鄰兩條側棱互相平行且相等。
側面展開圖
三稜柱側面展開圖如圖2所示：
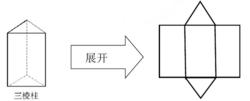圖2 三稜柱側面展開圖四稜柱側面展開圖如圖3所示：
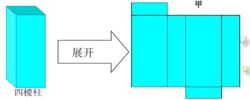圖3 四稜柱側面展開圖五稜柱側面展開圖如圖4所示：
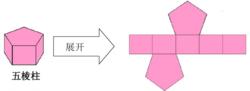圖4 五稜柱側面展開圖與正稜柱和斜稜柱的區別
1.與直稜柱的區別
直稜柱包含了正稜柱。直稜柱是所有側棱垂直於底面的稜柱，而正稜柱是在直稜柱的條件上加了上下底面必須是正多邊形。
2.與斜稜柱的區別
直稜柱的所有側棱都垂直與底面且各棱相互平行，上下兩個面沿豎直方向平移可重疊。但是斜稜柱的側棱不垂直與底面，與底面成一定的夾角，各棱都相互平行，上下兩個底面沿豎直方向平移不可重疊。
例題
一個食品包裝盒的側面展開圖如圖5所示，它的底面是邊長為2的正六邊形，這個包裝盒是什麼形狀的幾何體？試根據已知數據求出它的側面積。
解：根據圖示可知該包裝盒的側面是矩形，又已知上、下底面是正六邊形，因此這個幾何體是正六稜柱。
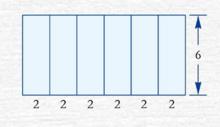圖5 例題展開圖由已知數據可知它的底面周長為2×6=12，
因此它的側面積為12×6=72。
