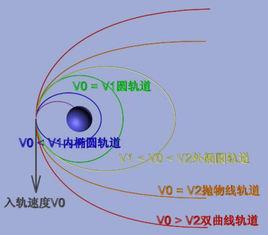
焦點弦概念
定義
焦點弦是指橢圓或者雙曲線或者拋物線上經過一個焦點的弦.
焦點弦簡述
數學中的弦是指同一條圓錐曲線或同一個圓上兩點連線而成的線段。
焦點弦特點
焦點弦是由兩個在同一條直線上的焦半徑構成的。焦半徑是由一個焦點引出的射線與橢圓或雙曲線相交形成的。而由於橢圓或雙曲線上的點與焦點之間的距離(即焦半徑長)可以用橢圓或雙曲線離心率和該點到對應的準線之間的距離來表示(圓錐曲線第二定義),因此,焦半徑長可以用該點的橫坐標來表示,與縱坐標無關。這是一個很好的性質。焦點弦長就是這兩個焦半徑長之和。此外,由於焦點弦經過焦點,其方程式可以由其斜率唯一確定,很多問題可以轉化為對其斜率範圍或取值的討論。(注意斜率不存在的情況!即垂直於x軸!)
研究對象
圓錐曲線方程。
橢圓焦點弦公式
2ab²/(b²+c²sin²α) (α為焦點弦的傾斜角)
2a±e(x1+x2)(焦點在x軸)
2a±e(y1+y2)(焦點在y軸)
雙曲線焦點弦公式
2ab²/lb²-c²sin²αl
拋物線焦點弦公式
x1+x2+p
拋物線焦點弦的其他結論
①弦長公式
②若直線AB的傾斜角為α,則|AB|=2p/sin²α
③y2=2px或y2=-2px時,x1x2=p²/4,y1y2=-p²
x2=2py或x2=-2py時,y1y2=p²/4,x1x2=-p²
性質套用
研究對象
圓錐曲線方程。圓錐曲線焦點弦的性質及其套用性質。
⑴過橢圓焦點F的直線交橢圓於A、B兩點,記q=a^2/c-c,是焦準距, e是離心率。
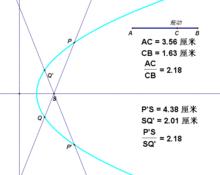 焦點弦
焦點弦⑵過雙曲線(a>0,b>0)焦點F的直線交雙曲線於A、B兩點,記p=c-a^2/c,是焦準距。若A、B兩點在雙曲線的同一支上,此時稱AB為雙曲線的同支焦點弦。若A、B兩點分別位於雙曲線的左支和右支上,此時稱AB為雙曲線的異支焦點弦。(拋物線的類似性質,本文從略)
證明舉例
(只證性質⑴,性質⑵的證明從略)由對稱性,不妨取F為右焦點。設右準線l與x軸交於點D,過A作AG⊥l於G,過B作BH⊥l於點H,則AG∥FD∥BH;且由橢圓的第二定義知,|AG|= ,|BH|= 。令|FE|=m,|ED|=n,則m+n=|FD|= 。故由 , = 可得:。∴ 。因此,m+n= ? 。∴ ,從而 就是焦準距。證畢。
[說明]①在上述證明過程中出現的“m = n”, “即|FE|=|ED|”,亦即 E為線段FD的中點(如圖1) 這是橢圓焦點弦的另一條性質。雙曲線與拋物線也有這一性質。
②如圖1,若設∠AFD= ,並分別過A、F作FD和BH的垂線,則可證: 從而得焦點弦長公式:|AB|= = 就是焦準距 。在雙曲線與拋物線中也有這樣的公式,如:在雙曲線 (a>0,b>0)中,若焦點弦AB的傾斜角為 ,則 , ;從而焦點弦長 為焦準距, 是離心率, 且 。③如圖1,若分別連線AD和BD,利用說明①的結論,則易證:∠ADF=∠BDF,即x軸平分∠ADB。在雙曲線與拋物線中也有這樣的結論。
例1 (07年全國(Ⅰ)高考(理)題)已知橢圓 的左、右焦點分別為F1、F2,過F1的直線交橢圓於B、D兩點,過F2的直線交橢圓於A、C兩點,且AC⊥BD,垂足為P。
(Ⅰ)設P點的坐標為(x0,y0),證明: ;
(Ⅱ)求四邊形ABCD的面積的最小值。
分析:(Ⅰ)略。
(Ⅱ)由(Ⅰ)知,AC⊥BD的垂足P在橢圓的內部,因此,(畫草圖)四邊形ABCD的面積S= 。
設直線AC的傾斜角為 ,則由本文性質的說明②可得:|AC|= ;而AC⊥BD,∴|BD|= 。從而S= 。
由均值不等式可得: ≤ 。
∴S≥ ,若且唯若 =45°或135°時取等號——問題獲解。
例子
求雙曲線
同支焦點弦的弦長的最小值;
⑵ 求雙曲線 異支焦點弦的弦長的最小值。
解 ⑴由對稱性(如圖2),不妨設同支焦點弦
AB經過右焦點F(c, 0) ,且設 = n,
則由本文性質⑴知: ,即 。
而mn≤ , ∴ ≥ 。
因此 ≥ ,即 ≥ 。
故|AB|=m+n≥ ,其中若且唯若m=n時取等號;即焦點弦AB垂直於實軸時,同支焦點弦的弦長取到最小值。
⑵設異支焦點弦CD的傾斜角為 ,則由本文性質的說明②可得: 。易知若且唯若 時取|CD|最小值2a。
(註:運用“數形結合”思想,也易從圖2中推出|CD|≥2a)。
如果拋物線兩條切線的交點在準線上,則切點弦必為焦點弦。
本文即在於用二次曲線的極線理論對這一性質作進一步的推廣,得出一些更一般的結論(即本文末的定理5和定理6)。
什麼是二次曲線的極線
設S:Ax+2Bxy+Cy+2Dx+2Ey+F=0為常態二次曲線,P(x0,y0)為不在S上的點(有心二次曲線的中心也除外,下同),我們把直線P:Ax0x+B(x0y+y0x)+Cy0y+D(x+x0)+E(y+y0)+F=0叫做點P關於S的極線,點P則叫做直線P關於S的極點。
在這樣的定義下,有心二次曲線的中心沒有極線,並且
定理1 (配極理論的原則). 若點P的極線通過點Q,則點Q的極線也通過點P.
定理2 通過一點P而且與一個常態二次曲線相切的直線它的切點在點P的極線上。
定理3 橢圓、雙曲線、拋物線焦點的極線是相應的準線。
定理4 如果橢圓、雙曲線、拋物線的兩條切線的交點在準線上,則過切點的直線必過焦點。
這是因為,焦點的極線是相應準線(定理3),又交點在準線上,準線上的點的極線就必過焦點(定理1),而定理2又告訴我們這條過焦點的極線恰好經過兩切點。
由於在射影平面內,圓的焦點是圓心,準線是無窮遠直線,故定理4又可推廣為:
定理5 如果常態二次曲線的兩條切線的交點在準線上,則過切點的直線必過焦點。
(特別:如果圓的兩條切線平行,則切點弦是圓的直徑)。
不言而喻,更一般還有
定理6 (1)點E是常態二次曲線內部一點,但不是有心二次曲線的中心,如果該曲線的兩條切線的交點在點E的極線上,則過切點的直線必過點E.
(2)如果有心二次曲線的兩條切線平行,則過切點的直線必過中心點。