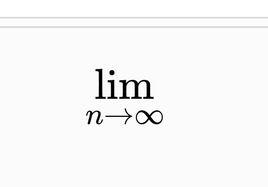定義
極限值指的是標準要求的數值範圍的界限，“極限值”也稱為”“極限數值”、“臨界值”、“界限數值”。
極限論是數學分析的基礎，極限問題是數學分析中的主要問題之一，中心問題有兩個：一是證明極限存在，極限問題是數學分析中的困難問題之一；二是求極限的值。
兩個問題有密切的關係：若求出了極限的值，自然極限的存在性也被證明。反之，證明了存在性，常常也就為計算極限鋪平了道路。本文主要概括了人們常用的求極限值的若干方法，更多的方法，有賴於人們根據具體情況進行具體的分析和處理。
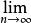極限值其通常表達式為：
函式關係
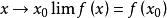極限值當函式在一點連續的時候，函式在這點的極限值等於函式值，所以；
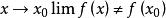極限值當函式在一點間斷的時候，函式在這點的極限值不等於函式值，所以。
特別注意：
1、函式在一點有極限與這點是否有定義無關.但是函式在這點的鄰域一定要有定義；
2、一般地，函式在一點有極限，是指函式在這點存在雙側極限,且相等，只有區間端點，是單側極限。
求極限值方法
求函式在一點的極限值有以下方法：
1、直接代入數值求極限；
2、約去不能代入的零因子求極限；
3、分子分母同除最高次冪求極限；
4、分子（母）有理化求極限；
5、套用兩個重要極限的公式求極限；
6、用等價無窮小量的代換求極限；
7、用洛必達法則求極限；
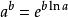極限值8、用換底公式 求極限。
