差集

設 G 為 v 階乘法群，單位元為 e，如果 D 為 G 的 k(0

簡介

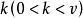差集

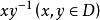差集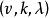

差集

差集

設 G 為 v 階乘法群，單位元為 e，如果 D 為 G 的 元子集，且形如 的元中含 G 的每個非單位元恰 次，則稱 D 為 G 的一個 差集。當 G 為阿貝尓群（即交換群）成循環群時，分別稱 D 為阿貝尓差集或循環差集。

套用

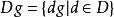差集

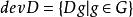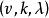差集

差集

差集

對於 G 中的元 g ，記，稱 Dg 為 D 關於 g 的平移。D 的所有平移的集合記為 devD，即。當 D 為一個 差集時，(G,devD) 是一個。因此，差集可以用來構造對稱區組設計。

另一方面，差集可以用來構造區有好的相關性質的序列。

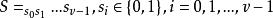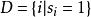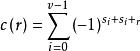差集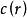

差集

差集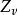

差集

差集

設 v 長二元序列。它的支撐集定義為 ，它的自相關函式(autocorrelation function) 定義為（下標按模 v 運算）。若序列 S 的自相關函式 只取兩個值，則稱序列 S 具有 2 級自相關函式。序列 S 具有 2 級自相關函式等價於 S 的支撐集 D 為模 v 剩餘類加群 的一個循環差集。