概念與定義
在數理統計中，要了解總體數據的分布規律，需要從總體中抽取一部分個體進行觀測。在抽樣過程中，每抽取一個個體，就是對總體X進行一次隨機試驗，抽取的n個個體XX…,X，稱為總體X的一個容量為n的樣本，樣本中所包含的個體數量稱為樣本容量。
樣本值：XX…,X，是n個隨機變數，抽取之後的觀測數據x,x…,x，稱為樣本值或子樣觀察值。
樣本特性
（1）代表性
子樣XX…,X的每個分量X，與總體X具有相同的機率分布。
（2）獨立性
每次抽樣的結果既不影響其餘各次抽樣的結果，也不受其他各次抽樣結果的影響。
常用統計量例舉
樣本的平均值稱為樣本均值，樣本偏離樣本均值的平方的平均值稱為樣本方差。樣本方差的算術平方根稱為樣本均方差。k階原點矩是指隨機變數偏離原點的距離的k次方的期望值，k階中心矩是指隨機變數偏離其中心的距離的k次方的期望值。
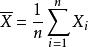樣本值（1）樣本均值：；
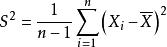樣本值（2）樣本方差：；
樣本值（3）樣本均方差或標準差：；
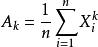樣本值（4）樣本的K階原點矩：；
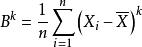樣本值（5）樣本的K階中心矩：；
套用
用樣本來估計總體，通過對樣本特徵的研究來估計總體的特徵。這種機率統計的方法在市場調研、金融評估等方面有廣泛的套用。
