預備知識
隨機現象
在自然界和人類社會中存在著兩類現象。
 樣本點
樣本點 樣本點
樣本點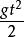 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點第一類,在一定條件下某種現象必定發生或必定不會發生,這類現象稱為確定性現象。例如,自由落體在經過 秒鐘後,落下的距離 必定是 ;在標準大氣壓下,水到攝氏600沸騰.第一種是必然會發生的,稱為必然事件,記作 ;第二種是必然不會發生的,稱為不可能事件,記作 。
另一類,在一定條件下,某種現象可能發生也可能不發生,稱這類現象為隨機現象。例如,杭州明年正月初一下雪;播種1000顆種子,有850顆發芽;發射一枚炮彈,彈著點與目標之問的距離為150米。
對隨機現象,在基本相同的條件下,重複進行試驗或觀察,可能出現各種不同的結果;試驗共有哪些結果事前是知道的,但每次試驗出現哪一種結果卻是無法預見的、這種試驗稱為隨機試驗(random experiment)。每次試驗不能預測其結果,這反映隨機試驗結果的出現具有偶然性;但如果進行大量重複試驗,所出現結果又具有某種規律性一統計規律性。例如,各次發射炮彈,彈著點與目標之間的距離可能各不相同,但如果射手技術較好,多次發射中距離近的必定是多數。
隨機試驗的可能結果稱為隨機事件(random event),簡稱事件。一次試驗中,某事件 A 可能發生,也可能不發生,發生的可能性有大有小。這一可能性大小的數量指標就是我們所要研究的事件的機率。
機率的統計定義
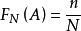 樣本點
樣本點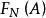 樣本點
樣本點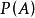 樣本點
樣本點在相同條件下重複做N次試驗,各次試驗互不影響。考察事件A出現的次數(頻數)n,稱 為在N 次試驗中出現的頻率(frequency)。頻率一般與試驗次數 N 有關,並且在 N 固定時,做若干組 N 次試驗,各組頻率一般也不相同;但當 N 很大時,頻率卻呈現某種穩定性,即 在某常數附近擺動,且當 N 無限增大時,頻率會“趨向”這個常數。這種規律稱為隨機現象的統計規律。很自然地,頻率所穩定到的那個常數可以表示事件 A 在一次試驗中發生的可能性的大小,稱作機率(probability),記為 ,機率的這種定義稱為統計定義。
雖然我們並不能由機率的統計定義確切地定出一個事件的機率,但是它提供了一種估計機率的方法,頻率與機率的關係就像物體長度的測量值與該長度之間的關係。物體的長度是客觀存在的,是該物體的固有屬性。測量值是它的某種程度的近似值。同樣,隨機事件發生的可能性大小機率是隨機事件的客觀屬性,多次隨機試驗所得的頻率則是它的某種程度的近似值。
必須注意,套用機率的統計定義時,各次試驗是在基本相同的條件下獨立進行的,而且次數要足夠多。
定義
 樣本點
樣本點隨機試驗的每一個基本結果稱為樣本點(sample point),通常記作 ω 。樣本點的全體稱為樣本空間(sample space),通常記作 。
樣本點和樣本空問是機率論中的兩個基本概念。隨著對所討論問題的興趣不同,同一隨機試驗可以有不同的樣本空間。討論問題前必須先確定樣本空間。
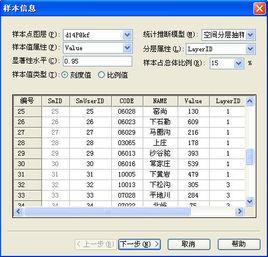
例1:口袋中裝有10個球:3個紅球,3個白球和4個黑球。
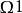 樣本點
樣本點任取1球,樣本空間可以取為 ={取得一個紅球,取得一個白球,取得一個黑球}。
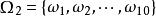 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點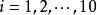 樣本點
樣本點若把球編號,紅球編為1~3號,白球和黑球分別為4~6和7~10號;則每取一球,必定是且只能是這些球號中的一個,故也可取樣本空間為 ,其中 ={取得第 號球), 。
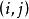 樣本點
樣本點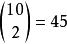 樣本點
樣本點如果每次共取兩個球.則每個樣本點可以用所取得的兩個球號 來表示,樣本空間可以是{(1,2),(1,3),….(1,10),(2,3),…,(2,10),...,(9,10)},共有 個樣本點,這是二維的樣本空間。
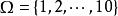 樣本點
樣本點例2:考察單位時間內落在地球上某一區域的宇宙射線數,這可能是0,也可能是1,是2,…,很難確定一個上界。於是可以取樣本空間為 。它包含無限多個樣本點,但可按一定的順序排列起來(稱為無限可列個)。
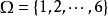 樣本點
樣本點例3:拋擲一枚骰子,雖然無法預知其結果如何,但總不外乎“出現1點”,“出現2點”,...,“出現6點”這六個基本的可能結果之一,其樣本空間 ,其中的1,2,3,4,5,6,就是六個樣本點。
樣本點計算
統計學家必須考慮和試圖解決的一個問題是,進行一次試驗時與某些事件的發生相關韻可能元素,這些問題屬於機率的研究範圍。在許多情況下,通過對樣本空間中的點計數,就可以解決機率問題,而不需要實際列出每一個元素。這種計數的基本原理通常稱為乘法規則。
乘法規則
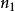 樣本點
樣本點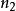 樣本點
樣本點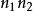 樣本點
樣本點如果完成一個操作有 種方法,對於這些方法,完成第二個操作有 種方法,則完成這兩個操作共有 種方法。
廣義乘法規則
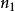 樣本點
樣本點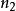 樣本點
樣本點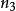 樣本點
樣本點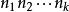 樣本點
樣本點如果完成一個操作有 種方法,對其中每一種方法的第二個操作有 種方法,對前兩步操作的每一種方法的第三個操作有 種方法,依次類推,則按順序完成 k 步操作有 種方法。
樣本點排序
 樣本點
樣本點對單個隨機變數進行處理,主要目的是使生成的各個變數的樣本點值能服從已知的機率分布函式。然而,各個隨機變數之間還有給定的相關關係,這種相關關係由隨機變數向量的相關係數矩陣來控制。為了使組合後的隨機變數樣本點序列能服從這種相關關係,需要專門研究樣本點的排序算法。由於隨機變數向量採用Nataf分布,在原變數空間或等效標準正態空間進行分析效果是相同的。這裡採用在等效標準正態變數空間上進行分析,相關關係由等效相關係數矩陣 控制,樣本點排序的疊代方法詳細分析過程敘述如下。
準備工作
 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點設有N維隨機變數向量 ,它們的邊際機率分布函式為 ,相關係數矩陣為 ,等效相關係數矩陣為,要求生成服從上述分布的N個樣本點。
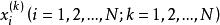 樣本點
樣本點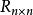 樣本點
樣本點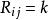 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點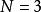 樣本點
樣本點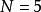 樣本點
樣本點 樣本點
樣本點首先對每個變數生成樣本點 ,接著用一個整數矩陣 來記錄所有樣本點的排序信息。 表示 變數在第 次抽樣的取值在該變數的所有抽樣點中排序為 , 取值範圍為1,2,…,N。在開始疊代之前將矩陣 任意賦初值。例如有三個隨機變數 ,要求生成的樣本點數量為 ,則 矩陣初始化後的一種可能形式為:
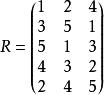 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點矩陣 提供的信息包含隨機向量的抽樣策略。共有個 行向量,每個行向量代表隨機變數向量的一次樣本實現。
疊代運算
 樣本點
樣本點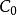 樣本點
樣本點(1)根據 矩陣的信息生成隨機變數向量樣本集,通過統計分析可得到它的初始協方差矩陣 ;
 樣本點
樣本點 樣本點
樣本點(2)將 個樣本點向量轉換到等效標準正態變數空間,得到相應標準正態變數向量 的樣本點集
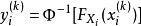 樣本點
樣本點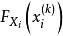 樣本點
樣本點為簡化分析,其中各個樣本點的機率分布函式 實際上可以近似地從該點的序號得出:
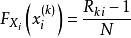 樣本點
樣本點 樣本點
樣本點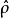 樣本點
樣本點 樣本點
樣本點(3)對進行統計分析,得到相應的相關係數矩陣,將進行矩陣變換:
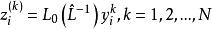 樣本點
樣本點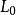 樣本點
樣本點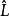 樣本點
樣本點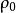 樣本點
樣本點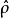 樣本點
樣本點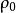 樣本點
樣本點式中,和分別為和的Cholesky分解下三角矩陣,為目標等效相關係數矩陣。
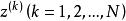 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點 樣本點
樣本點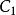 樣本點
樣本點(4)根據的大小順序來更新矩陣,並由矩陣重新對隨機變數向量的個樣本進行排序。對所得到的樣本進行統計分析,得到相應的協方差矩陣。
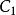 樣本點
樣本點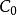 樣本點
樣本點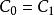 樣本點
樣本點(5)將中的各元素和進行對比,如果兩矩陣所有元素的差的絕對值都小於容許值,則認為疊代收斂,退出疊代,否則並回到步驟(2)繼續疊代.
各個變數的樣本點生成過程為確定性的,即每次抽樣過程得到的樣本集都是不變的。與此不同的是,樣本排序的結果往往是隨機的。
算法的收斂性分析
由樣本點集統計出的隨機變數相關係數是一個統計量,它只能接近原機率模型的真實值,而不能時刻等於真實值。傳統的用隨機模擬法生成的樣本所對應的係數是一個具有機率背景的統計量,能以機率論證明:相關係數的統計量作為一種特殊的隨機變數,當樣本點數量逐漸增大時,其樣本實現等於真實值的機率將趨近於1。與傳統隨機模擬法不同的是,Latin hypercube法是從算法角度確保相關係數統計量的合理性。但是,它是否也具備傳統抽樣方法的性質呢?為了說明這一點,下面分析一個實際例子。
 相關係數統計量的誤差和樣本量的關係
相關係數統計量的誤差和樣本量的關係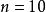 樣本點
樣本點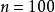 樣本點
樣本點設隨機變數向量服從獨立標準常態分配,即實際相關係數矩陣應為單位矩陣,非主對角元素為0。採用前面說明的算法生成樣本,並計算協方差矩陣統計量。由於目標協方差矩陣中非主對角元素應為零,所以將協方差統計量矩陣中非對角元素中的最大值,作為絕對誤差值。當隨機變數數目分別為及時,誤差值隨樣本數目大小的變化規律計算結果見右圖。由圖所示的分析結果可知,此處採用的疊代算法同樣具備收斂性質,即相關係數統計量和真實值的誤差隨樣本量的增大而降低;從圖中的結果還可發現,Latinhypercube法的相關係數統計量誤差和隨機變數數量無關。