樣本的定義
實際中很多不確定現象都可以用隨機變數描述,而套用中的一個十分重要的問題是找到隨機變數的分布或其數字特徵。 例如:某進出口貿易公司進口了10萬台微型計算器,按產品技術規定,使用壽命小於4000小時即為次品,且次品率大於1% 就不接受這批產品。如何得知這批產品的次品率呢?是否要測量每一台計算器呢?顯然,這是不現實的,解決這個問題的好辦法就是隨機抽樣,然後根據抽樣檢驗得到的次品率來估計整批產品的次品率。也就是從10萬台產品中按隨機原則,抽取一部分(假如100件)產品組成一個樣本,由樣本(100件產品)次品率推斷整批產品的次品率。
這裡,我們把被觀察對象的全體(本例中的10萬台計算器)稱作總體,把從總體中隨機抽取的(被抽中的100台計算器)小群體稱作樣本,而樣本中所包含的個體單位數目稱為樣本容量(100個)。
對於這批計算器,我們關心的是它的使用壽命(低於4000小時的比例有多少)的分布,設X表示“任一台計算器的使用壽命”,它是一個隨機變數,我們把隨機抽中的100件產品看作是100個隨機變數X1,X2……,X100,每一個計算器的使用壽命都是一個隨機變數,一旦測試完畢,測試的結果就是100個觀測值x1,x2,……x100,統計抽樣的任務就是根據測試結果x1,x2,……x100來估計總體X的分布情況。
我們作如下概括:設X是一個隨機變數,X1,X2……,Xn是一組相互獨立與X具有相同分布的隨機變數,稱X為總體,X1,X2……,Xn為來自總體的簡單隨機樣本,簡稱樣本,n為樣本容量,稱樣本觀察值為樣本值,由於按隨機原則取樣,在試驗之前,人們無法知道試驗的結果,所以X1,X2……Xn,是一組隨機變數,而在試驗之後,得到一組X1,X2……,Xn的觀察值x1,x2,……xn,,它們則是一組確定的數值。
樣本統計量與樣本分布
總體實際上就是一個隨機變數X,有一定的機率分布和分布的數字特徵。由於總體分布的數字特徵往往也就是機率分布函式中的參數(如常態分配的數學期望和方差就是密度函式中的參數μ和σ;二項分布的數學期望和方差就是參數np和npq等),所以根據樣本信息估計總體數字特徵就稱為參數估計。在進行參數估計時,我們並不是直接用一個個的具體樣本值來估計、推測總體參數,而是根據樣本值得出的一些特定的量,來估計總體參數的。由樣本得出的特定的量就稱為統計量,用數學的術語說,統計量就是樣本的函式,它只依賴於樣本,不包含任何未知參數。根據樣本X1,X2……,Xn,可以計算樣本均值和樣本方差。樣本均值 和樣本方差都是統計量,因為它們都是樣本的函式,且不含未知的參數。樣本統計量是隨著樣本不同而變化的量,由於樣本是隨機樣本,所以樣本統計量也是一個隨機變數。顯然,樣本均值 隨著抽取的樣本不同而變化,是一個隨機變數,既然是一個隨機變數就有一定的機率分布,我們把樣本統計量的分布稱作抽樣分布。
如上例,10萬台微型計算機是我們研究的總體,隨機抽取的100台組成一個樣本,由於任意100台都可組成一個樣本,所以被抽中的100台是一個隨機樣本,由樣本計算的均值(方差、成數等)也是隨機變數,這些由樣本計算的特徵值,稱為樣本統計量。
樣本分布函式
總體的分布函式稱為總體分布函式.從總體中抽取容量為n的樣本,得到n個樣本觀測值,設其中互不相同的觀測值由小到大依次為, 則有頻率分布表
定義樣本分布函式
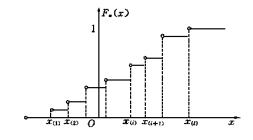
其中和式是對小於x的一切的頻率求和,的圖形如圖1所示.
樣本分布函式的性質
(1)
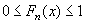
(2)
是非減函式;
(3)
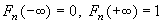
(4)
在每個觀測值處左連續,且在跳躍間斷點處的躍度等於頻率.
