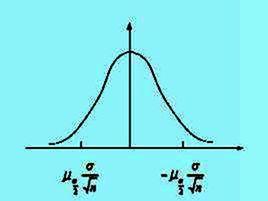
簡介
樣本平均數是從一個或多個隨機變數上的數據集合（樣本）計算的統計量。樣本平均值是總體平均值的估計量，其中總體是指採集樣本的集合。
樣本平均數是一個向量，每個元素是隨機變數之一的樣本均值，即每個元素是其中一個變數的觀察值的算術平均值。如果僅觀察到一個變數，則樣本平均數是單個數字（該變數的觀察值的算術平均值）。
由於其易於計算和其他期望的特徵，樣本平均數廣泛用於統計和套用中，以表示分布的位置。
計算方法
設x是第j個隨機變數（j = 1，...，K）的第i個獨立觀察值（i = 1，...，N）。 這些觀察結果可以排列成N列向量，每個都有K個子項，K×1列向量給出所有變數的第i個觀察值，表示為x（i = 1，...，N）。
樣本平均數
樣本平均數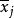樣本平均數向量是一個列向量，它的第j個元素是第j個變數的N個觀察值的平均值 ：
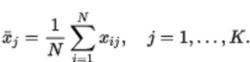樣本平均數因此，樣本平均數包含每個變數的觀察值的平均值，並被寫入
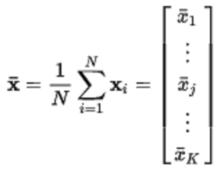樣本平均數樣本平均數的差異
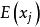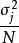樣本平均數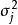
樣本平均數
樣本平均數對於每個隨機變數，樣本平均數是人口平均值的一個很好的估計量，其中“良好”估計量被定義為有效和無偏差。 當然，由於從同一分布中抽取的不同樣本將給出不同的樣本平均數，因此對真實均值的估計不同，估計量可能不是群體平均值的真實值。 因此，樣本平均數是隨機變數，而不是常數，因此具有其自身的分布。 對於第j個隨機變數的N個觀察值的隨機抽樣，樣本均值的分布本身具有等於群體平均值和方差等於，其中是隨機變數X的方差。
相關知識
如果求出的平均數是由所研究對象全部數據求出的，就叫做總體平均數；如果是由樣本求出的，就叫做樣本平均數。可以用樣本平均數去估算總體平均數.
計算方法：（1）若 ， ，…， ，則 (a—常數， ， ，…，接近較整的常數a)；
（2）加權平均數：
（3）平均數是刻劃數據的集中趨勢(集中位置)的特徵數。
通常用樣本平均數去估計總體平均數，樣本容量越大，估計越準確。
