四大分類
素數p 階循環群Zp
除了單位元群和它本身以外沒有其他正規子群的有限群。有限單群可比喻為搭成有限群的”積木塊“,是有限群結構的基石。它長期是群論研究的中心問題。
① 素數 p 階循環群Zp,它包括了所有的交換單群。
交錯群
② n個文字的所有偶置換構成的交錯群 An,當 n≥5時是非交換單群。
李型單群和李型群
李型群是複數域上單李群在有限域上的相似物,不全是單群。它包括有限域上某些典型群、例外群和扭群。前兩者也稱為謝瓦萊群,共有9個族,它們的記號是 Aq), n≥1; Bq), n>1; Cnq), n>2; Dnq), n>3; G2q); F4q); E6q); E7( q); E8q)。這q= pm, p是素數。以下的 q也有此意義。
除了 A1(2)、 A1(3)、 B2(2)、 G2(2)外,這些群對其中心的商群都是有限單群。這些群中的大部分,E.伽羅瓦、C.若爾當、L.E.迪克森等已早有研究。直到1955年,C.謝瓦萊對任意有限域 GFq)構造出複數域上單李群的相似物,用統一的方法證明了這些群的存在性、單純性和其他性質。
扭群共七族,它們是2An(),n>1;2B2(),=2;2Dn(),n>3;3D4(q);2G2(),=3;2F4(),=2;2E6()。除了2A2(2)、2B2(2)、2G2(3)、2F4(2)外,它們都是單群。而2F4(2)的換位子群(2F4(2))┡還是不在以上幾族中的一個特殊單群。 利用謝瓦萊群的圖自同構和域自同構可以統一地得到所有扭群,如R.施坦伯格、鈴木通夫、R.雷和J.蒂茨等人的工作。 在以上群中An()、Bn()、Cn()、2An()分別同構於GF()上的典型群PSLn+1()、PΩ2n+1()、PSP2n()和PSUn()。而Dn()和2Dn()分別同構於和(對每個 有兩族2n維的正交群,以“+”和“-”兩個符號來區別)。謝瓦萊群中的G2()、F()、E6()、E7()、E8()則是例外群。
零散單群
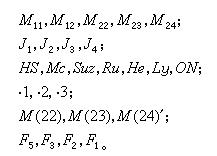 公式
公式凡不屬於以上三類的有限單群, 稱為零散單群,共有26個。É.L.馬蒂厄於1860年和1873年先後得到5個多重傳遞置換群M11(4重)、M12(5重)、M22(3重)、M23(4重)和M24(5重),它們都是零散單群。一百年之後,Z.簡科於1965年才發現了另一個新的零散單群,記為J1。爾後陸續地發現了所有的零散單群,仿照前者,一般以重要發現者的姓的前面字母來記各零散單群,若同一人發現多於一個這樣的群時則加上數字的下標,它們是 最大的零散單群為 F1,名為怪物群或魔群,它的階為2^46·3^20·5^9·7^6·11^2·13^3·17·19·23·29·31·41·47·59·71,約為10^54。G.格里斯用手算,從47·59·71=196883維的線性表示而得到 F1。它有著良好的內在的幾何結構,並且有20個左右的零散單群作為它的子群,所以並不是什麼怪物,G.格里斯改稱它為“友好巨人”。
研究有限單群的一般方法,可非常概括地歸結為以下幾種:
①模特徵標論和特殊特徵標論方法,前者為R.(D.)布饒爾所創,後者為布饒爾和鈴木通夫所創。
② p局部子群分析法。它是由J.G.湯普森等人建立和發展起來的研究非單位 p子群的正規化子的方法。
③幾何分析法及其發展。此法是由B.費希爾和M.阿施布歇爾等所創。
完全分類
綜述
即找出有限單群所有的同構類,經全世界上百名的數學家約40年的共同努力,終於在1981年得到解決,這是數學史上的又一個非凡成就。有限單群分類的整個論證用了5000頁以上的篇幅,散布在超過300篇文章之中,引用了很多新的群論概念和證明了大量的定理。歷史上的一些重要進展,可以概述如下:
歷史發展
20世紀初,W.伯恩賽德關於 pαqъ階群(p、是素數)必是可解群的定理,是有限單群分類問題早期最重要的工作。它說明非交換有限單群的階至少有三個不同的素數。三四十年代之交,布饒爾開始利用他所創造的模特徵標理論來研究有限單群問題,在這期間,段學復隨布饒爾研究了階含素數p僅為一次的群及其模特徵標,1942年,他們一起完成了10000階以下的單群分類。1945年合寫了“論有限單群”的論文。他們的一些結果至今還被人引用,有的得到推廣。1954年布饒爾關於對合的中心化子的定理,即設τ是偶階單群G的一個對合即二階元素,CG(τ)是其中心化子,則。於是,從已知偶階單群的對合的中心化子出發,最多構造出有限多個單群。可用這結果去發現和構造一些新單群,許多零散單群就是這樣發現的;更重要的是可以用中心化子來刻劃群的構造,用於單群分類。這一定理標誌了單群分類的新起點,而被稱之為布饒爾綱領。布饒爾是近代有限單群分類工作的先驅。 1962年,W.費特和湯普森關於奇階群必為可解群的定理是單群分類中最重要的一個定理,它標誌著有限單群分類的重大突破,也是第一篇長文章(225頁之多)。湯普森在文中初步建立並運用了p局部子群分析法,其後於1968~1974年間,他在關於極小單群(即所有真子群皆為可解群)及更一般的單N群(即所有p局部子群皆為可解群)的分類定理的證明中,完善了 p局部子群分析法。
1972年,D.戈朗斯坦提出的有限單群分類方案或計畫,指出了如何才能實現有限單群的完全分類。雖然這個計畫在後來作了某些修改,但是此後美、英、德、日等國的群論學家自發地組織起來按計畫去攻克這個大問題,終於以10年左右的時間取得了數學史上的這項重大的成果。
有限單群分類問題的解決對有關問題的影響非常深遠,有些長期存在的群論問題已經由於它的解決而解決或可以解決。例如,
①O.施賴埃爾猜想有限單群的外自同構群是可解的。
②有限單群皆可由兩個元素生成;有限非交換單群的元素皆為換位子。
③除Sn和An外,不存在k≥6重傳遞置換群;所有雙重傳遞群已被決定;所有素數p次置換群已知。
下述有限單群問題正在被研究並取得進展:
①整理和簡化有限單群分類問題的全部論證。
②研究F1和模函式的關係,進而研究哪些單群能作為有理數域上的伽羅瓦群。
③用分類的結果去解決群論以及其他的數學問題,這種套用正迅速增加。
④進一步計算有限單群的常、模特徵標和子群等。