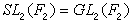典型群
正文
線性群、正交群、辛群和酉群的總稱。這些群自19世紀以來就是討論研究較多的。1946年，H.外爾的《典型群》一書出版後，於是人們通常把這些群稱為典型群。線性群 線性變換組成的群。線性變換與矩陣是一一對應的,也可看作是矩陣組成的群。設K是體,n>1,K上n×n可逆矩陣的全體對矩陣乘法組成一群，稱為K上n次一般線性群，記作 GLn(K)。將 GLn(K)的換位子群記作SLn(K)，稱之為K上n次特殊線性群。當K是域時,除n=2,K=F2 (F2是2個元素的域)的情形外,SLn(K)就是GLn(K)中行列式等於1的矩陣組成的群，而
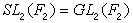。將 GLn(K)和 SLn(K)模其各自的中心的商群，分別記作PGLn(K)和PSLn(K),並分別稱為K上n次射影一般線性群和K上n次射影特殊線性群。 正交群 設F是特徵不為2的域，S是F上n×n非奇異對稱矩陣。 F上一切 n×n矩陣T 適合條件T┡ST=S(T┡是T的轉置)者對矩陣的乘法組成一群，稱為 F上（由S 定義的）n 次正交群,記作On(F,S)。On(F,S)中行列式等於1的矩陣組成的子群記作
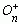(F,S),而On(F，S)的換位子群記作Ωn(F,S)。On(F,S)、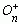(F,S)和Ωn(F,S)模其各自中心的商群，分別記作 POn(F，S)，P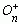(F，S)和PΩn(F,S)。 當F是特徵為2的域時，如果S是一n×n正則矩陣,即S 定義的二次型 X┡SX （這裡
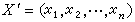是X的轉置）是非退化的，用Kn表示 F上一切n×n交錯矩陣的全體組成的模，那么F 上一切 n×n 矩陣T 適合條件T┡ST呏S(modKn)者對矩陣乘法組成一群，稱為F上(由S定義的)n次正交群，記作On(F，S)，這時On(F,S)定義為On(F,S)中可表為偶數個On(F,S)中剩餘數為1的元素之積的那些矩陣所組成的子群,Ωn(F,S)仍定義為On(F,S)的換位子群。所謂n×n矩陣T 的剩餘數，是指T-I的秩，這裡 I是n×n 單位矩陣。和特徵不為2的情形一樣, 可類似地定義POn(F,S),POn(F,S)和PΩn(F,S)。 辛群 設J是域F上2n×2n非奇異交錯矩陣,F上的一切2n×2n矩陣T 適合條件T┡JT=J者對矩陣乘法組成一群，稱為F上（由J 定義的）2n次辛群，記作SP2n（F,J）。SP2n(F,J)模其中心的商群稱為F上2n次射影辛群，記作PSP2n(F,S)。
酉群 設H 是體K上n×n非奇異埃爾米特矩陣,K 有一對合性反自同構τ，即 τ 是從K 到K 之上的一一映射，且滿足條件
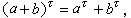
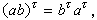
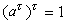。K上一切 n×n矩陣T 適合
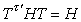者組成一群,稱為K上（由H 定義的）n維酉群，記作Un(K,H)。 Un(K,H)中酉平延生成之群記作TUn(K,H)。所謂酉平延,是指對於 Un(K,H)中的元素T,T-I是秩為1的冪零陣。這裡I是n×n單位矩陣。將Un(K,H)和 TUn(K,H)模其各自中心的商群，分別記作PUn(K,H)和PTUn(K,H)。
實數域和複數域上的典型群在19世紀就開始出現在幾何學和物理學中。由於它們在幾何學和物理學中的重要性，如O幦(F,I)是三維歐氏空間的鏇轉群,O4(F,S)是相對論中的洛倫茨群,這裡S 是對角線上依序為1，1，1，-1的對角陣。19世紀末更發現它們在復單李群和實單李群分類中是幾個大類型的單李群的突出地位，從而在數學中一直受到重視與研究。最初研究它們的方法是李群方法,後來則出現純代數方法,主要研究它們的結構、自同構和同構、表示等問題。
典型群的結構，在19世紀末的李群研究中，已知道SLn(R)，On(R,I)等是實單李群，於是人們就想到考察有限域上的典型群是否能得到有限單群，而有限單群的獲得與研究始終是有限群論的中心問題之一。到20世紀40年代,更將典型群的基域推廣到任意體上,從而得到無限單群。以線性群為例,設K 是任意體,則除開PSL2(F2)、PSL2(F3)之外，PSLn(K) 都是單群。對其他類型的典型群也有相當的結果，但對於正交群和酉群，當S 和H 定號時,PΩn(F，S)和PTUn(K，H)何時是單群的問題還沒有完全解決。所謂F上n×n非奇異對稱矩陣S 定號,是指X′SX＝0蘊涵X＝0。
典型群的自同構和同構,除遺留少數情形外,各類型的典型群的自同構均被確定。仍以線性群為例，當n≥2時，GLn(K)的自同構必為以下兩種形狀之一:
，
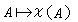
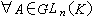或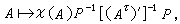
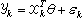，其中P∈GLn(K),σ和τ分別為R 的自同構和反自同構,(Aτ)┡是(Aτ)的轉置,這裡ⅹ(A)為將GLn(K)映入它的中心的一個同態。在自同構的形狀還沒有被確定的群中，有SL2(K)（K為特徵0的體）、Ωn(F,S)(S定號)等。關於典型群間的同構,特別是單典型群間的同構，也還有一些情形沒有被確定。 典型群的表示，是內容極為豐富的一個領域，運用李群方法（包括李代數方法和緊李群上不變積分方法）研究典型群的表示，已有悠久的歷史和豐富的成果，同時也還有許多重要問題值得研究。從20世紀50年代中開始的有限域上典型群的表示論的研究，也是當代十分活躍的一個領域；至於基域是一般域或體時，典型群的表示則幾乎沒有被研究。
近代，典型群的結構和自同構的研究已被推廣到環上,特別是交換環上。數環（包括整數環和代數整數環）上的典型群是所謂的算術群，由於它牽涉的面很廣，已成為近代數學的重要分支。
華羅庚在典型群的結構和自同構的研究中有自己獨特的矩陣方法，他和中國其他數學工作者運用這一方法取得了一系列的成果，受到國際上的重視，被稱為中國學者的矩陣方法。
參考書目
華羅庚、萬哲先著：《典型群》，上海科學技術出版社，上海，1963。
J.Dieudonné,Sur les Grupes Classiques, 2éed., Springer-Verlag, Berlin, 1971.
H.Wey1,Classical Groups, Princeton Univ Press, Prince-ton, 1939.
