正文
交換群作為特殊類型的群，也有諸如元素的階、群的階、子群、商群等概念以及相應的結果（見群）。在交換群中，子群和正規子群是相同的概念，習慣上把交換群的運算記作加法，用0表示群的單位元素,用-α表示元素α的逆元素,用nα表示α的n次冪,交換群的直積改稱為直和。
有限非交換群有複雜的結構，至今還不完全清楚。然而有限交換群卻有著非常簡單的結構。1878年，F.G.弗羅貝尼烏斯等證明了下面的基本定理：任一有限交換群G可表成有限個且階為素數冪的循環群的直和，即
，其中k是自然數，Gi 是循環群且
,pi是素數，ni是自然數，並且數k和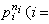
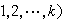是由群G完全確定的。這個定理是一個具有典型意義的結構定理。關於有限交換群的子群、商群、自同態等問題，都可以利用這個定理去解決。因而，交換群理論的主體是研究無限群。 對於具有有限個生成元的無限交換群G都可表成有限個循環群的直和：
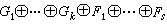其中Gi是循環群且,pi是素數,ni是自然數。而Fj都是無限循環群；且非負數k,s以及
由群G惟一確定。這是對於有限交換群基本定理的一個完滿的推廣。 以上兩個定理是一系列研究的起點，啟示人們考慮還有哪些群類（更一般地，模類）可表為循環群（循環模）的直和，這樣的群類具有什麼性質，等等。
n個（有限個或無限個）無限循環群的直和G，稱為自由交換群或自由群，其個數(基數)n是群的不變數,稱為自由群G的秩。自由群在交換群理論中所占的地位,與非交換自由群在一般群理論中的地位相當，即任意一個群A總可看成自由群的同態像。為此，只要取定群A的一個生成元集
，並相應地取符號集{xα,α ∈I}，以xα為生成元可作無限循環群<xα>，再作它們的直和即得自由群G=嘰<xα>。G中元素都可惟一寫成有限和形式
是整數。因此，可作映射 
若干個循環群的直和G具有與自由群類似的一些性質。例如，這樣的直和G的子群,也是一些循環群的直和；當把G表成無限循環群與階為素數冪的循環群的直和時，這種表法在同構意義下是惟一的，即其中無限循環群的個數與階為素數冪
的循環群個數都由G本身惟一確定。 每一元都是有限階（無限階）的交換群，稱為周期群(無扭群)。既含有有限階元又含有無限階元的群，稱為混合群。每一元的階都是素數p的冪的群,稱為準素群或p準素群。
除群是個重要的而且已被完全刻畫了的群類。所謂除群G,是指對於任意自然數n和任意元素α,方程nx=α都有解的群G。不難驗證,全體有理數關於數的加法作成一個無扭除群；而對於固定的素數p及所有自然數n，一切pn次單位根的全體關於複數的乘法作成p準素群P，它也是除群，並記作p∞型群。任意除群都是若干個有理數加群和若干個p∞型群（對某些素數p）的直和。R.貝爾指出除群具有如下特性:若群G含有一個除子群h（即h本身是除群）,則h必是G的直和項,即有子群K使G=h嘰K。反之，具有如下性質的群h必是除群：若h是群G的子群，則h必是G的直和項。除群是模論中重要的入射模概念的一個原型。不含除子群的群，稱為簡約群。對任意交換群的研究可歸結為對簡約群的研究。
交換群G中有限階元素的全體可作成一子群h，稱為G的周期子群,而商群G/h是無扭群。周期群G中階為素數p之冪的元素的全體G(p)是G的子群,且有
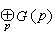(p取遍所有素數)。因此，周期群的研究可歸結為準素群的研究。設G是p準素群,對自然數n規定
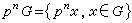。易知,pnG是子群,且有
。設非零元素α∈G，若有n使得α∈pnG,而
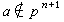G,就把n稱為α的高。否則，就說α的高是∞。因此,α的高就是使方程pmx=α在G中有解的最大自然數m(或∞)。高是交換群論中最重要的概念之一。除群中每一元素的高都是∞，而循環群的直和中則沒有高為∞的元素。 重要的普呂菲爾定理給出一些可表為循環群的直和的某些群類：①若G是p準素群且有n使pnG={0},則G是循環群的直和。②若G是可數(即|G|是可數基數)p準素群，但是它不含高為∞的元素，則G是循環群的直和。
含有高為∞的元素的群不可能表成循環群的直和，對此需另尋刻畫方法。H.厄爾姆在20世紀30年代作出了影響深遠的貢獻。他對p準素群G引入了定義在序數集上取值基數的一個函式ƒG(α) (後來稱之為厄爾姆不變數)，給出了重要的厄爾姆定理:兩個可數p準素群G和h是同構的，若且唯若它們有相同的厄爾姆不變數，即對所有的序數α，有ƒG(α)=ƒH(α)。近年來,這個定理在I.卡普蘭斯基和E.沃克等人手中得到進一步的推廣。例如，對於一類所謂完全投射群，相應的結論也成立。
對於無扭群，秩是一個最基本的概念，它類似於向量空間的維數。如果對於群G的有限個元素α1,α2,…,αn有不全是零的整數k1,k2,…,kn,使得
,就說α1,α2,…,αn是相關的，否則就說是無關的。如果G的一個子集S的任意有限子集都是無關的，就說S是無關的。群G的所有極大無關子集具有相同的基數，稱為G的秩。秩為1、2的無扭群的結構基本上已清楚，例如,秩為1的無扭群恰為有理數加群的一切子群。其他一些無扭群也作過研究，例如完全分解無扭群以及它們的純子群。總之，對無扭群的研究遠不如對周期群的研究深入。 混合群G總可以看成周期群A藉助無扭群B的擴張。最初的一些研究，常集中於如下的問題：在什麼條件下這個擴張G是可裂的,即有G=A嘰B成立。R.貝爾給出一個結果：若混合群G的周期子群A是一些除群和一些階小於某固定n的循環群的直和，則G是可裂的。近年來，I.卡普蘭斯基、R.B.沃菲爾德等找到了一些方法，能從整體上討論混合群，從而開創了一個新局面。
任一交換群都可看成整數環上的模，為此只需引入模運算n·g=g+…+g(n個)即可。交換群作為特殊的模，為一般模論提供了大量的概念和定理的原型，例如張量積就是其中之一。交換群G的自同態對應全體End(G)關於自同態的乘法和加法作成一個環,而交換群G可以自然地看成End(G)的任意子環上的模。交換群、模論、環論是互相密切聯繫的。
參考書目
I.Kaplansky，Infinite Abelian Groups，Revised ed.,Univ.of Michigan Press, Ann Arbor, 1969.
L.Fuchs,Infinite Abelian Groups，Vol.1～2，Academic Press,New York,1970,1973.
