基本概念
線段:至少由三筆組成,而且前三筆必須有重疊的部分。
線段劃分定理:線段被終結,若且唯若至少被有重疊部分的連續三筆的其中一筆終結。而只要構成有重疊部分的前三筆,那么必然會形成一線段。換言之,線段終結的充要條件,就是形成新線段。
概念要點
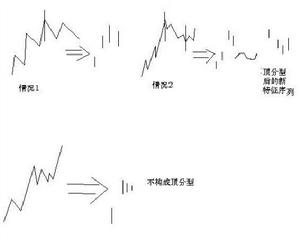
1、線段至少有連續的三筆(可以更多),但並不是連續的三筆就一定構成線段,這三筆必須有重疊的部分。如圖①②是線段的最基本形態。
2、線段無非有兩種,從向上一筆開始的,和從向下一筆開始的。從向上一筆開始的線段,其終結也是向上一筆,其頂gi一定大於第一筆的底d1,故該線段是向上的;同理從向下一筆開始的線段,其方向也是向下的。如圖①②。

4、用S代表向上的筆,X代表向下的筆。
以向上筆開始的線段,可以用筆的序列表示:S1X1S2X2S3X3…SnXn。容易證明,任何Si與Si+1之間,一定有重合區間。而考察序列X1X2…Xn,該序列中,Xi與Xi+1之間並不一定有重合區間,因此,這序列更能代表線段的性質。

把每一元素看成是一K線,那么,如同一般K線圖中找分型的方法,也存在所謂的包含關係,也可以對此進行非包含處理。經過非包含處理的特徵序列,成為標準特徵序列。

分析理解
線段劃分的標準參照一般K線圖關於頂分型與底分型的定義,可以確定特徵序列的頂和底。注意,以向上筆開始的線段的特徵序列,只考察頂分型;以向下筆開始的線段,只考察底分型。
在標準特徵序列里,構成線段終點分型的三個相鄰元素,只有兩種可能:
第一種:特徵序列為頂分型中,第1和第2二元素間不存在特徵序列的缺口,那么該線段在該頂分型的高點處結束,該高點是該線段的終點;底分型反之亦然。
第二種:特徵序列為頂分型中,第1和第2元素間存在特徵序列的缺口,如果從該分型最高點開始向下一筆開始形成的特徵序列出現底分型(意味形成了新的線段),那么該線段在該頂分型的高點處結束,該高點是該線段的終點;底分型反之亦然。
強調,在第二種情況下,後一特徵序列不一定封閉前一特徵序列相應的缺口,而且,第二個序列中的分型,不分第一二種情況,只要有分型就可以。(見下圖)
假設某轉折點是兩線段的分界點,然後對此用兩種情況去考察線段劃分是否滿足,如果滿足其中一種,那么這點就是真正的線段的分界點;如果不滿足,那就不是,原來的線段依然延續。特徵序列的分型中,第一元素就是以該假設轉折點前線段的最後一個特徵元素,第二個元素,就是從這轉折點開始的第一筆,顯然,這兩者之間是同方向的。因此,如果這兩者之間有缺口,那么就是第二種情況,否則就是第一種,然後根據定義來考察就可以。這裡還要強調一下包含的問題。上面的分析知道,在這假設的轉折點前後那兩元素,是不存在包含關係的,因為,這兩者已經被假設不是同一性質的東西,不一定是同一特徵序列的;但假設的轉折點後的頂分型的元素,是可以套用包含關係的。為什麼?因為,這些元素間,肯定是同一性質的東西,或者就是原線段的延續,那么就同是原線段的特徵序列中,或者就是新線段的非特徵序列中,反正都是同一類的東西,同一類的東西,當然可以考察包含關係。
實例
如圖⑤,6屬於第一種情況,所以6是線段結束;同理15也屬於第一種情況;9-10和11-12是包含關係,處理後為等同於11-10,所以點11不是線段的分界點;故該圖有三段,分別是1-6,6-15和15-20。

