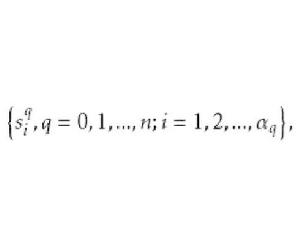基本介紹
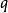 有向單形
有向單形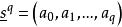 有向單形
有向單形 有向單形
有向單形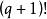 有向單形
有向單形 有向單形
有向單形 有向單形
有向單形 有向單形
有向單形一個 維單形 ,它的 個頂點有 個不同次序的排列,當 時,這些排列可分成兩組,同組的任意兩個排列相差偶數個對換,不同組的任意兩個排列相差奇數個對換,這兩組排列稱為單形 的兩個定向。換言之,根據頂點次序是奇排列還是偶排列分成兩組,稱為 的兩個定向,並且稱為互為相反的定向。
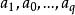 有向單形
有向單形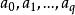 有向單形
有向單形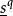 有向單形
有向單形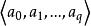 有向單形
有向單形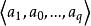 有向單形
有向單形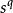 有向單形
有向單形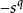 有向單形
有向單形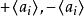 有向單形
有向單形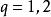 有向單形
有向單形指定一個定向的單形稱為 有向單形。例如,排列 與 就確定了 的兩個相反定向,相應的兩個有向單形分別記為 與 ,若把一個記為 ,則另一個就記為 ,對於零維單形只有一個頂點,為統一起見用 表示它的兩個定向,有向單形在 時分別是有向線段和有向三角形。為區別起見,原來的單形可稱為 無向單形。單純復形是幾何對象,而群是代數對象,從復形過渡到它的同調群,關鍵是單形的定向與邊緣運算元這兩個概念 。
相關定義與定理
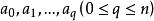 有向單形
有向單形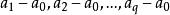 有向單形
有向單形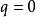 有向單形
有向單形設 是 R 中的點,若 具有線性關係,則說明這一組點占有最廣的位置。當 時就是一個點,自然此點占有最廣位置 。
單純形
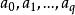 有向單形
有向單形 有向單形
有向單形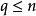 有向單形
有向單形 有向單形
有向單形設 是 R 中占有最廣位置的 點,而 ,則我們稱點 的集合
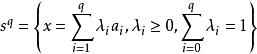 有向單形
有向單形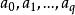 有向單形
有向單形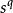 有向單形
有向單形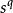 有向單形
有向單形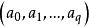 有向單形
有向單形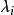 有向單形
有向單形為 q維 單純形,簡稱 q維單形, 稱為 頂點,故常將 記作 ,而係數 稱為此單純形的 重心坐標。
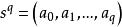 有向單形
有向單形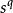 有向單形
有向單形 有向單形
有向單形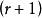 有向單形
有向單形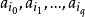 有向單形
有向單形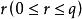 有向單形
有向單形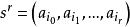 有向單形
有向單形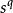 有向單形
有向單形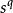 有向單形
有向單形定義 對於q維單形 ,稱 的( )個頂點中的 個點 所構成的 維單形 為 的一個r維面, 的0維面就是頂點,把1維面稱為棱。
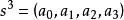 有向單形
有向單形 有向單形
有向單形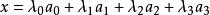 有向單形
有向單形例1 考慮3維單形,對於點,就有,
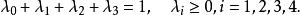 有向單形
有向單形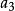 有向單形
有向單形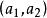 有向單形
有向單形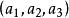 有向單形
有向單形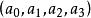 有向單形
有向單形例如,維面,為棱,為面,為體,如圖1所示。
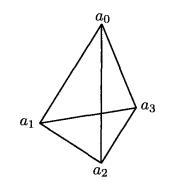 圖1 3維單形(四面體)
圖1 3維單形(四面體)有向單形與無向單形
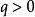 有向單形
有向單形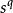 有向單形
有向單形 有向單形
有向單形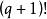 有向單形
有向單形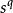 有向單形
有向單形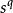 有向單形
有向單形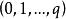 有向單形
有向單形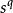 有向單形
有向單形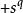 有向單形
有向單形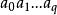 有向單形
有向單形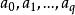 有向單形
有向單形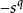 有向單形
有向單形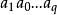 有向單形
有向單形當 時, 的 點有 個排列,它們決定同一個 ,這樣的單形 被稱為 無向單形,在 排列中,有一半是偶置換,一半是奇置換,因而這兩個置換等價類構成了 兩個定向,指定一個定向單形稱為 有向單形,簡記“”=,這裡指頂點次序為的有向單形;另一個定向單形記作“”=,以單純形作為構件,可以組成單純複合形、多面體和鏈。
單純複合形(復形)
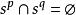 有向單形
有向單形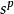 有向單形
有向單形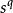 有向單形
有向單形如果或是一個公共面,則單形和是 規則相處的,如圖2所示,否則是 不規則相處的,如圖,3所示。
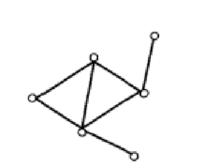 圖2 規則相處
圖2 規則相處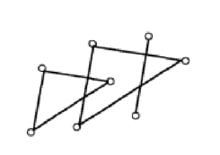 圖3 不規則相處
圖3 不規則相處設W是 R 中有限個單形集合,如果W滿足下列兩個條件:
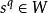 有向單形
有向單形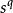 有向單形
有向單形(1)如果,的任一面也屬於W;
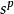 有向單形
有向單形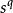 有向單形
有向單形(2)W的任意兩個單形和規則相處,
則稱W為 單純複合形,簡稱為 復形,如圖4所示;否則是 非復形,如圖5所示。
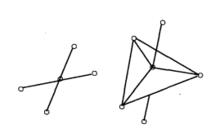 圖4 復形
圖4 復形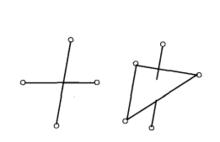 圖5 非復形
圖5 非復形有向單形的基本組
設W是一個n維復形,它的全體無向單形
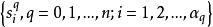 有向單形
有向單形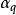 有向單形
有向單形都己任意地規定了一個定向,這裡為W中q維單形的個數,這樣,得到一組有向單形
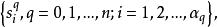 有向單形
有向單形上式稱為W的 有向單形的基本組。
鏈
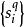 有向單形
有向單形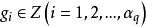 有向單形
有向單形設為n維復形W的一個基本組,對於,形式地定義
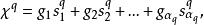 有向單形
有向單形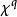 有向單形
有向單形稱為W的一個 q維鏈。
1維鏈可看作是有向的折線 。
鏈邊界
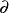 有向單形
有向單形如果把邊界運算元擴展到有向單形和復形上去,則有下面的鏈邊界。
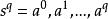 有向單形
有向單形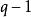 有向單形
有向單形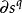 有向單形
有向單形定義 對於任意q維有向單形,我們定義()維鏈:
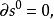 有向單形
有向單形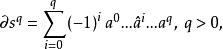 有向單形
有向單形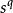 有向單形
有向單形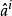 有向單形
有向單形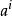 有向單形
有向單形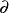 有向單形
有向單形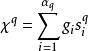 有向單形
有向單形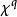 有向單形
有向單形稱之為的 邊界鏈或簡稱 邊界。式中表示缺這一點,也可以把擴展到W的q維鏈上去,定義W的任意q維鏈的邊界為
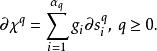 有向單形
有向單形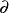 有向單形
有向單形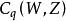 有向單形
有向單形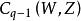 有向單形
有向單形由此可見,邊界運算元建立了鏈群到的一個同態 :
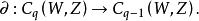 有向單形
有向單形