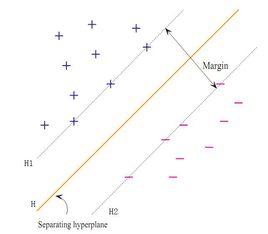
概念
工程設計中最最佳化問題（optimization problem）的一般提法是要選擇一組參數（變數），在滿足一系列有關的限制條件（約束）下，使設計指標（目標）達到最優值。因此，最最佳化問題通常可以表示為以下的數學規劃形式的問題。
最最佳化問題對於一組可用列向量表示的變數，我們的目的是
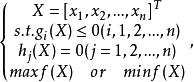最最佳化問題
最最佳化問題
最最佳化問題
最最佳化問題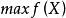
最最佳化問題
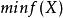最最佳化問題
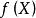最最佳化問題式中的是“”的縮寫，表示“在約束條件之下”。和是指目標函式取最大值或最小值。
因此，進行工程最佳化設計時，應將工程設計問題用上述形式表示成數學問題，再用最最佳化的方法求解。這項工作就是建立最佳化設計的數學模型。
基本原理
設計變數與設計空間
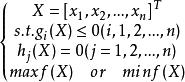最最佳化問題 最最佳化問題
最最佳化問題
最最佳化問題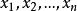 最最佳化問題
最最佳化問題
最最佳化問題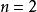
最最佳化問題
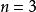最最佳化問題式子中的是維實數空間（記為）中的一個向量，它由個分量組成。它是在最最佳化過程中變化而決定設計方案的量，即在最最佳化中需要進行選擇的一組數值，稱為設計變數向量。從幾何上講，每個變數向量就是以各變數分量為坐標軸的變數空間的一個點。當時，即只有一個變數分量，這個變數沿直線變化；當時，即只有兩個變數分量時，這個變數向量的所有點組成一平面；而當時，組成立體空間。有三個以上變數分量時，則構成多維空間。設計空間的每一個設計變數向量對應於一個設計點，即對應於一個設計方案。設計空間包含了該項設計的所有可能方案。
目標函式
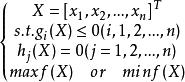最最佳化問題 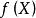最最佳化問題式子中的稱為目標函式。它是設計變數向量的實值連續函式，通常還假定它有二階連續偏導數。目標函式是比較可供選擇的許多設計方案的依據，最最佳化的目的就是要使它取極值。在變數空間中，目標函式取某常值的所有點組成的面稱為等值面。即它是使目標函式取同一常數值的點集：
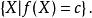最最佳化問題 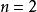最最佳化問題當，即只有兩個變數分量時為等值線。
等值面具有以下性質：
（1）有不同值的等值面之間不相交。因為目標函式是單值函式。
（2）除了極值點所在的等值面以外，不會在區域的內部中斷。因為目標函式是連續函式。
（3）等值面稠密的地方，目標函式值變化得比較快；稀疏的地方變化得比較慢。
（4）一般地說，在極值點附近等值面近似地呈現為通信橢圓面族。
