概述
組合最最佳化問題（combinatorial optimizationproblem）是一類在離散狀態下求極值的問題。把某種離散對象按某個確定的約束條件進行安排，當已知合乎這種約束條件的特定安排存在時，尋求這種特定安排在某個最佳化準則下的極大解或極小解的間題。組合最最佳化的理論基礎含線性規劃、非線性規劃、整數規劃、動態規劃、擬陣論和網路分析等。組合最最佳化技術提供了一個快速尋求極大解或極小解的方法。
基本原理
組合最最佳化是通過對數學方法的研究去尋找離散事件的最優編排、分組、次序或篩選等，是運籌學中的一個經典且重要的分支，所研究的問題涉及信息技術、經濟管理、工業工程、交通運輸、通信網路等諸多領域。該問題可用數學模型描述為：
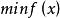組合最最佳化問題
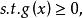組合最最佳化問題
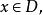組合最最佳化問題
組合最最佳化問題
組合最最佳化問題
組合最最佳化問題
組合最最佳化問題其中，為目標函式，為約束函式，為決策變數，表示有限個點組成的集合。
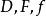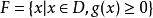組合最最佳化問題 組合最最佳化問題
組合最最佳化問題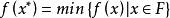
組合最最佳化問題 組合最最佳化問題
組合最最佳化問題
組合最最佳化問題
組合最最佳化問題 組合最最佳化問題 組合最最佳化問題一個組合最最佳化問題可用三參數（）表示，其中表示決策變數的定義域，表示可行解區域，中的任何一個元素稱為該問題的可行解，表示目標函式。滿足的可行解稱為該問題的最優解。組合最最佳化的特點是可行解集合為有限點集。由直觀可知，只要將中有限個點逐一判別是都滿足的約束和比較目標值的大小，該問題的最優解一定存在和可以得到。因為現實生活中的大量最最佳化問題是從有限個狀態中選取最好的，所以大量的實際最佳化問題是組合最最佳化問題。
