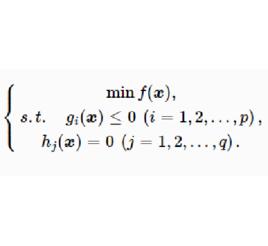基本介紹
約束最最佳化問題(constrained optimization problem)是指具有約束條件的非線性規劃問題。極小化問題的一般形式為
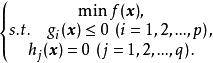約束最最佳化問題僅有等式約束條件的約束最最佳化問題，可採用消元法、拉格朗日乘子法或罰函式法，將其化為無約束最最佳化問題求解；對於含有等式約束和不等式約束條件的最最佳化問題，可採用以下方法：將不等式約束化為等式約束；將約束問題化為無約束問題；將非線性規劃問題用線性逼近的方法來近似求解；在可行域中沿某方向作一維搜尋，尋求最優解 。
約束最最佳化問題的解法
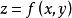約束最最佳化問題
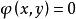約束最最佳化問題約束最最佳化問題就是求目標函式 滿足約束條件 的極值問題。因此，約束最最佳化，也稱 條件極值 。
約束最最佳化問題的解法有兩種：
化約束最最佳化問題為無約束最最佳化問題
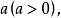約束最最佳化問題例1 最大面積 設長方形的長、寬之和等於 問長方形的長、寬如何設計，才能使面積最大?
解: 這就是一個約束最最佳化問題：設長方形的長為x，寬為y，求目標函式A=xy在條件x+y=a之下的最大值。
由於從約束條件x+y=a中容易解出y=a-x，代入目標函式
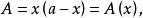約束最最佳化問題問題歸結為求一元函式A(x)的極值。
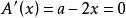約束最最佳化問題
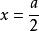約束最最佳化問題 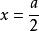約束最最佳化問題
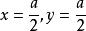約束最最佳化問題
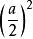約束最最佳化問題由 ，得駐點 。這是實際問題，最值一定存在，則 就是最大值點。因此，當 時，長方形面積最大，其最大值為 。
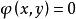約束最最佳化問題
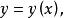約束最最佳化問題
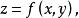約束最最佳化問題從上述例子可以看出化約束最最佳化問題為無約束最最佳化問題的思路：從約束條件 中解出 並將它代人目標函式 於是，問題就轉化為求一元函式
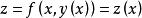約束最最佳化問題的無約束最最佳化問題。
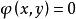約束最最佳化問題但是，這種方法有局限性，因為有時從約束條件 中解出y或x並非易事。因此，下面介紹另一種方法 。
拉格朗日乘數法
這一方法的思路是：把求約束最最佳化問題轉化為求無約束最最佳化問題，看它應該滿足什麼樣的條件?
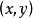約束最最佳化問題 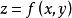約束最最佳化問題 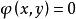約束最最佳化問題
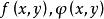約束最最佳化問題
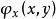約束最最佳化問題
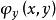約束最最佳化問題 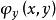約束最最佳化問題 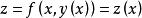約束最最佳化問題設 是函式 在約束條件 下的約束最最佳化問題的極值點。如果函式 在點(x，y)的鄰域內有連續偏微商，且 、 不全為0(不妨設 ≠0)，則根據費馬引理，一元函式 在點x的微商
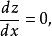約束最最佳化問題由隱微分法，有
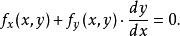約束最最佳化問題
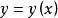約束最最佳化問題 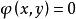約束最最佳化問題而 是由 所確定，所以
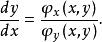約束最最佳化問題
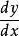約束最最佳化問題代入上式，消去 ，得
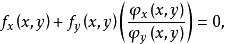約束最最佳化問題即
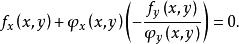約束最最佳化問題
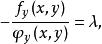約束最最佳化問題令 則有
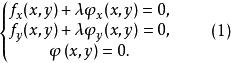約束最最佳化問題稱滿足此方程組(1)的點(x，y)為 可能極值點。
為了便於記憶，並能容易地寫出方程組(1)，我們構造一個函式
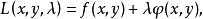約束最最佳化問題
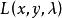約束最最佳化問題稱 為 拉格朗日函式。則方程組(1)可以記為
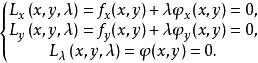約束最最佳化問題於是，我們把用拉格朗日乘數法求解約束最最佳化問題的步驟歸納如下：
①構造拉格朗日函式
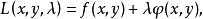約束最最佳化問題
約束最最佳化問題稱為 拉格朗日乘數；
②解方程組
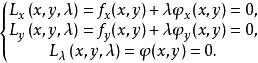約束最最佳化問題得點(x，y)為可能極值點；
③根據實際問題的性質，在可能極值點處求極值 。
