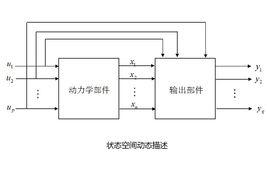
基本概念
狀態變數
足以完全表征系統運動狀態的最小個數的一組變數為狀態變數 。
狀態空間
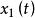 最小實現
最小實現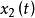 最小實現
最小實現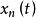 最小實現
最小實現以狀態變數 , ,…, 為坐標軸所構成的n維空間,稱為狀態空間。
一般系統的動態特性可以由狀態變數所構成的一階微分方程組來描述 。
實現問題
由描述系統輸入輸出動態關係的運動方程或傳遞函式,建立系統的狀態空間表達式的問題,稱為實現問題 。
最小實現
在實現問題中,若原傳遞函式沒有零極點對消的情況,則對該傳遞函式的實現稱為 最小實現 。
狀態空間的建立
狀態空間的建立,或者說其表達式的建立,一般有幾種途徑:
已有系統框圖時,可以將系統框圖轉換為模擬結構圖,把圖中每個積分器的輸出選為狀態變數,就可以通過模擬結構圖直接寫出系統狀態空間表達式(狀態方程和輸出方程);
對於相對簡單、機理清晰的系統,可以從系統的機理出發,利用物理規律和數學方法直接建立狀態空間表達式;
在不知道系統的內部結構的情況下,通常是僅有系統的外部描述——傳遞函式或運動方程,此時即系統的實現問題,實現本身是非唯一的,將在下面詳細介紹(僅討論最小實現問題)。
1.已有系統框圖時,可以將系統框圖轉換為模擬結構圖,把圖中每個積分器的輸出選為狀態變數,就可以通過模擬結構圖直接寫出系統狀態空間表達式(狀態方程和輸出方程);
2.對於相對簡單、機理清晰的系統,可以從系統的機理出發,利用物理規律和數學方法直接建立狀態空間表達式;
3.在不知道系統的內部結構的情況下,通常是僅有系統的外部描述——傳遞函式或運動方程,此時即系統的實現問題,實現本身是非唯一的,將在下面詳細介紹(僅討論最小實現問題)。
求取最小實現
基本流程
一般的求取傳遞函式陣G(s)的最小實現的步驟是:
1)對於給定的傳遞函式陣G(s),先初選出一種實現(A,B,C),通常最方便的方法是選取能控標準型實現或者能觀標準型實現;
2)對於上面初選的實現,找出其完全能控且完全能觀的部分,於是這個完全能控能觀的部分就是給定的傳遞函式陣W(s)的最小實現。
實現方法
假設n階線性系統傳遞函式為
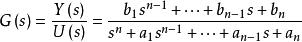 最小實現
最小實現其中Y(s)是輸出函式的拉氏變換,U(s)是輸入函式的拉氏變換,a和b都是實數。三種常用的實現方法如下 :
1.標準型法
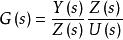 最小實現
最小實現①對G(s)引入中間變數z(t),改寫G(s)為 ;
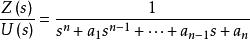 最小實現
最小實現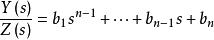 最小實現
最小實現②令 ,則 ,其微分方程為
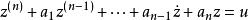 最小實現
最小實現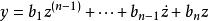 最小實現
最小實現③可選取z及其一系列導數為狀態變數,則有
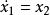 最小實現
最小實現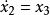 最小實現
最小實現……
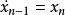 最小實現
最小實現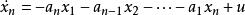 最小實現
最小實現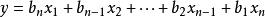 最小實現
最小實現輸出方程:
④根據以上方程可以得到系統的狀態空間表達式。
2.串聯法
該方法的基本思路是把一個n階傳遞函式分解為若干一階傳遞函式的 乘積,再分別對各個一階環節模擬,最後 串聯得到系統狀態變數模擬圖。
3.並聯法
該方法的基本思路是把一個n階傳遞函式分解為若干一階傳遞函式的 累加,再分別對各個一階環節模擬,最後 並聯得到系統狀態變數模擬圖。