定義
最小相位系統(minimum-phase system)在一定的幅頻特性情況下，其相移為最小的系統，也稱最小相移系統。這種系統的系統函式（亦稱網路函式或傳遞函式）與非最小相位系統相比，二者的幅頻回響特性是相同的，但前者的相位絕對值則較後者為小。在保持系統函式的幅頻回響特性不變的情況下，使其相位最小的充分必要條件是：對於模擬信號系統，要求其零點(即使系統函式為零的復頻率值)僅位於S平面（即復 頻域平面）的左半平面或虛軸上；對於離散信號系統，則要求其零點僅位於Z平面（即離散信號復頻域平面)的單位圓內或單位圓上。常可用於進行相位校正。
對於連續時間系統，如果控制系統開環傳遞函式的所有極點和零點均位於s左半平面上，則稱該系統為最小相位系統。對於離散時間系統，則是所有零極點均位於單位圓內。
一個系統被稱為最小相位系統，若且唯若這個系統是因果穩定的，有一個有理形式的系統函式，並且存在著一個因果穩定的逆函式。
特點
最小相位系統主要有以下2個特點：
1、如果兩個系統有相同的幅頻特性，那么對於大於零的任何頻率，最小相位系統的相角總小於非最小相位系統；
2、最小相位系統的幅頻特性和相頻特性直接關聯，也就是說，一個幅頻特性只能有一個相頻特性與之對應，一個相頻特性只能有一個幅頻特性與之對應。對於最小相位系統，只要根據對數幅頻曲線就能寫出系統的傳遞函式。
性質
最小相位系統主要有以下3個性質：
1、如果假設一個最小相位系統有系統函式H(z)，那么，它具有下列性質：
•所有的極點在單位圓內
•所有的零點在單位圓內
•假設h(n)為最小相位系統的集中在n較小的範圍內。
•最小相位系統的對數譜的實部和虛部構成一對希爾伯特變換。由此，可以通過幅頻特性推出最小相位系統的相頻特性，反之亦然。
•給定H(z)為穩定的因果系統，若且唯若H(z)為最小相位系統時，其逆系統才是穩定和因果的。
•任何一個非最小相位因果系統，都可以由一個最小相位系統和一個全通系統級聯而成。
2、從最小相位系統的幅頻回響，它具有下列性質：
•一組具有相同幅頻回響的因果，穩定的濾波器中，最小相位濾波器對於零相位具有最小的相位偏移。
•不同的離散時間系統可能具有相同的幅頻回響，如果h(n)為相同幅頻的離散時間系統的單位抽樣回響，單位抽樣回響的的能量集中在n為較小值的範圍內。一個因果穩定的，並且具有有理形式系統函式的系統一定可以分解成一連串全通系統和最小相位系統。
工程上常用這一性質來消除失真，但是缺點是它消除了幅度失真後會帶來相移失真。
從傳遞函式角度看,如果說一個環節的傳遞函式的極點和零點的實部全都小於或等於零,則稱這個環節是最小相位環節，如果傳遞函式中具有正實部的零點或極點，或有延遲環節，這個環節就是非最小相位環節。
3、表達時(泰勒級數展開)，會發現它具有正實部零點。
最小相位系統具有如下性質：
•最小相位系統傳遞函式可由其對應的開環對數頻率特性確定；反之亦然。
•最小相位系統的相頻特性可由其對應的開環頻率特性確定；反之亦然.
•在具有相同幅頻特性的系統中,最小相位系統的相角範圍最小。
•最小相位系統有一條性質很好理解：其逆系統也是穩定的，因為最小相位系統的逆系統的極點就是原來系統的零點，還是在Z平面的單位圓內，所以仍然是穩定的。
•最小相位系統的相位延遲最小：這個我的理解是通過S平面來看的，對於系統的相位延遲，假設極點的偏移是W1,W2,W3...零點的偏移是Q1,Q2,Q3；那么總的偏移應該是兩類偏移各自相加然後做減法：對於最小相位系統，其零點極點都在S平面的左半平面，最後減法兩者抵消，得出來的值（也就是相位的改變）較小，而最大相位系統恰恰相反，極點和零點在不同的半平面，相減得出的值較大，也就是系統的相位變化較大。似乎這個才應該是最小（最大）相位相位系統的名字的來由。
•任何非最小相位系統可以表示成 H(z)=Hmin(z)·Hap(z)，這個也能明白，Hmin(z)是所有零點在S平面左平面，Hap(z)是在右平面。
判斷方法
判斷系統是否為最小相位系統的簡單方法是：如果兩個系統的傳遞函式分子和分母的最高次數都分別是m，n，則頻率ω趨於無窮時，兩個系統的對數幅頻曲線斜率均為－20（n－m）dB/dec但對數相頻曲線卻不同：最小相位系統趨於－90°（n－m），而非最小相位系統卻不這樣。
比較
最小相位系統與非最小相位系統舉例舉例比較最小相位系統和非最小相位系統。假設有兩個系統G1（s）和G2（s），其傳遞函式見表。
G1（s）為最小相位系統，G2（s）為非最小相位系統，0< Tz< TpoG1（s）和G2（s）的幅頻特性相同，但相頻特性不同。
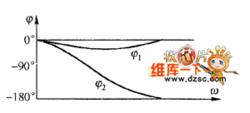最小相位系統G2（s）的一個RHP零點與G1（s）的I－HP零點成鏡像，圖為最小相位系統G1（s）與非最小相位系統G2（s）的相頻特性的比較。由圖可知，0< ω< ∞，相位|Φ1（ω）|<|Φ2（ω）|。最小相位系統的相頻特性，其相角變化範圍是最小的，而非最小相位系統的相位滯後嚴重。
相關區別
最小相位系統：所有的零點都在單位圓內的傳輸函式即為最小相位系統。或者說，一個系統函式為H(Z)的系統，如果本身和其逆系統均為因果穩定系統，那么H(Z)即為最小相位系統。判斷方法也很簡單：如果一個H(Z)的分母的解都小於1，這樣的系統就是最小相位系統。另外提一句，所有的零點都在單位圓外的系統就是最大相位系統
全通系統：如果一個輸入進入一個系統，輸出的時候所有頻率分量的幅度均不發生任何改變，這樣的系統就是全通系統。一個信號進入全通系統後所有頻率分量的幅度不改變，但相位可能會發生改變，這也是為什麼很多系統要級聯全通系統的原因，因為前面的系統將相位改變了，後面就要級聯全通系統對相位進行修正。全通系統其實也很好識別，有他的特徵的。就是分母和分子的係數是倒序的。也即所有的零極點對在Z平面上都是復共軛的。
任何有理系統函式都能表示成一個最小相位系統和一個全通系統的組合。H(Z)=Hmin(Z)Hap(Z)。
全通系統與最小相位系統通常用來進行頻率回響的補償。
假定失真系統是穩定且因果的，系統函式為Hd(Z)，若要實現完全補償，那么補償系統Hc(Z)必須是Hd(Z)的逆系統。如果進一步要求Hc(Z)也為穩定且因果，那么只有當Hd(Z)是最小相位系統才有可能。
假設我們已知失真系統Hd(Z)要找出其補償系統Hc(Z)。首先需要將Hd(Z)中全部位於單位圓外的零點反射到單位圓內其共軛倒數的位置上（即最小相位/全通分解）得到一個最小相位系統Hdmin(Z)。且有：
Hd(Z) = Hdmin(Z)*Hap(Z)
那么我們就可以選取補償系統的系統函式為：
Hc(Z) = 1/Hdmin(Z)
這樣就完全補償了頻率回響，並且相位回響具有Hap(ejw)的變化 。
