問題定義
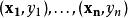序列最小最佳化算法
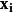序列最小最佳化算法
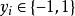序列最小最佳化算法SMO算法主要用於解決支持向量機目標函式的最最佳化問題。考慮數據集 的二分類問題，其中 是輸入向量， 是向量的類別標籤，只允許取兩個值。一個軟邊緣支持向量機的目標函式最最佳化等價於求解以下二次規劃問題的最大值：
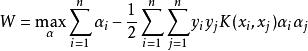序列最小最佳化算法滿足：
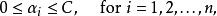序列最小最佳化算法
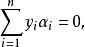序列最小最佳化算法
序列最小最佳化算法
序列最小最佳化算法其中， 是SVM的參數，而 是核函式。這兩個參數都需要使用者制定。
算法
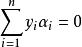序列最小最佳化算法
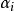序列最小最佳化算法
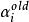序列最小最佳化算法
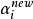序列最小最佳化算法SMO是一種解決此類支持向量機最佳化問題的疊代算法。由於目標函式為凸函式，一般的最佳化算法都通過梯度方法一次最佳化一個變數求解二次規劃問題的最大值，但是，對於以上問題，由於限制條件 存在，當某個 ，從 更新到 時，上述限制條件即被打破。為了克服以上的困難，SMO採用一次更新兩個變數的方法。
數學推導
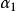序列最小最佳化算法
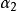序列最小最佳化算法假設算法在某次更新時更新的變數為 和 ，則其餘變數都可以視為常量。為了描述方便，規定
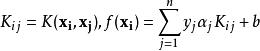序列最小最佳化算法
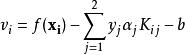序列最小最佳化算法因而，二次規劃目標值可以寫成
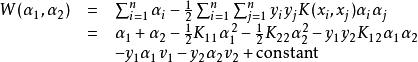序列最小最佳化算法 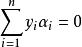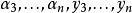序列最小最佳化算法
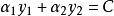序列最小最佳化算法
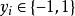序列最小最佳化算法 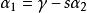序列最小最佳化算法
序列最小最佳化算法
序列最小最佳化算法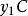
序列最小最佳化算法
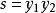序列最小最佳化算法 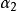序列最小最佳化算法由於限制條件 存在，將 看作常數，則有 成立（ C為常數）。由於 ，從而 ( 為變數 ， ）。取 為最佳化變數，則上式又可寫成
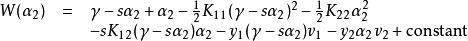序列最小最佳化算法 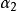序列最小最佳化算法對 求偏導以求得最大值，有
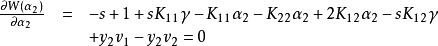序列最小最佳化算法因此，可以得到
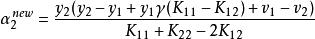序列最小最佳化算法
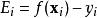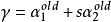序列最小最佳化算法
序列最小最佳化算法
序列最小最佳化算法規定誤差項 ，取 ，並規定 ，上述結果可以化簡為
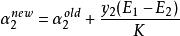序列最小最佳化算法
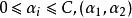序列最小最佳化算法
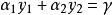序列最小最佳化算法
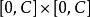序列最小最佳化算法
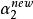序列最小最佳化算法再考慮限制條件 的取值只能為直線 落在 矩形中的部分。因此，具體的SMO算法需要檢查 的值以確認這個值落在約束區間之內 。
算法框架
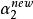序列最小最佳化算法
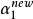序列最小最佳化算法
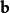序列最小最佳化算法 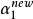序列最小最佳化算法 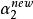序列最小最佳化算法SMO算法是一個疊代最佳化算法。在每一個疊代步驟中，算法首先選取兩個待更新的向量，此後分別計算它們的誤差項，並根據上述結果計算出 和 。最後再根據SVM的定義計算出偏移量 。對於誤差項而言，可以根據 、 和b的增量進行調整，而無需每次重新計算。具體的算法如下：
序列最小最佳化算法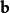 序列最小最佳化算法1、隨機數初始化向量權重 ，並計算偏移量
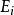序列最小最佳化算法2、初始化誤差項
3、 選取兩個向量作為需要調整的點
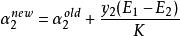序列最小最佳化算法4、令
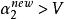序列最小最佳化算法5、如果
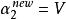序列最小最佳化算法6、令
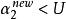序列最小最佳化算法7、如果
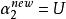序列最小最佳化算法8、令
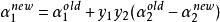序列最小最佳化算法9、令
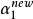序列最小最佳化算法 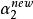序列最小最佳化算法 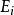序列最小最佳化算法 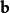序列最小最佳化算法10、 利用更新的 和 修改 和 的值
11、如果達到終止條件，則停止算法，否則轉3
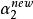序列最小最佳化算法其中，U和V為 的下界和上界。特別地，有
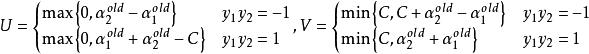序列最小最佳化算法 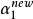序列最小最佳化算法
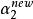序列最小最佳化算法
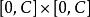序列最小最佳化算法這一約束的意義在於使得 和 均位於矩形域 中。
最佳化向量選擇方法
可以採用啟發式的方法選擇每次疊代中需要最佳化的向量。第一個向量可以選取不滿足支持向量機KKT條件的向量，亦即不滿足
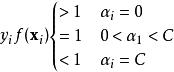序列最小最佳化算法
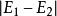序列最小最佳化算法的向量。而第二個向量可以選擇使得最大的向量。
終止條件
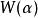序列最小最佳化算法SMO算法的終止條件可以為KKT條件對所有向量均滿足，或者目標函式增長率小於某個閾值，即
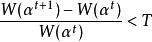序列最小最佳化算法