介紹
偏最小二乘用於查找兩個矩陣( X和 Y)的基本關係,即一個在這兩個空間對協方差結構建模的隱變數方法。偏最小二乘模型將試圖找到 X空間的多維方向來解釋 Y空間方差最大的多維方向。偏最小二乘回歸特別適合當預測矩陣比觀測的有更多變數,以及 X的值中有多重共線性的時候。相比之下,標準的回歸在這些情況下不見效(除非它是Tikhonov正則化)。
偏最小二乘算法被用在偏最小二乘路徑建模中,一個建立隱變數(原因不能沒有實驗和擬實驗來確定,但一個典型的模型會基於之前理論假設(隱變數影響衡量指標的表現)的隱變數模型)這種技術是結構方程模型的一種形式,與經典方法不同的是基於組件而不是基於協方差。
偏最小二乘來源於瑞典統計學家Herman Wold,然後由他的兒子Svante Wold發展。偏最小二乘的另一個詞(根據Svante Wold)是 投影到潛在結構,但偏最小二乘法依然在許多領域占據著主導地位。儘管最初的套用是在社會科學中,偏最小二乘回歸被廣泛用於化學計量學和相關領域。它也被用於生物信息學,sensometrics,神經科學和人類學。而相比之下,偏最小二乘回歸最常用於社會科學、計量經濟學、市場行銷和戰略管理。
偏最小二乘法是集主成分分析、典型相關分析和多元線性回歸分析3種分析方法的優點於一身。它與主成分分析法都試圖提取出反映數據變異的最大信息,但主成分分析法只考慮一個自變數矩陣,而偏最小二乘法還有一個“回響”矩陣,因此具有預測功能。
研究認為,集多元線性回歸分析、典型相關分析、主因子分析等方法於一體的偏最小二乘回歸方法( PLS) 更適用於FM 分析, 可以避免數據非常態分配、因子結構不確定性( factor indeterminacy) 和模型不能識別等潛在問題。
底層模型
偏最小二乘的一般多元底層模型是
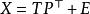 偏最小二乘回歸法
偏最小二乘回歸法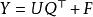 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法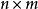 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法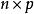 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法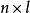 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法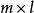 偏最小二乘回歸法
偏最小二乘回歸法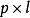 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法其中 是一個 的預測矩陣, 是一個 的回響矩陣; 和 是 的矩陣,分別為 的投影(“X分數”、“組件”或“因子”矩陣)和 的投影(“Y分數”); 和 分別是 和 的正交 載荷矩陣,以及矩陣 和 是誤差項,服從獨立同分布的常態分配隨機變數。對 和 分解來最大化 和 之間的協方差。
算法
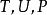 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法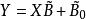 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法 偏最小二乘回歸法
偏最小二乘回歸法偏最小二乘的許多變數是為了估計因子和載荷矩陣 和 。它們中大多數構造了 和 之間線性回歸的估計。一些偏最小二乘算法只適合 是一個列向量的情況,而其它的算法則處理了 是一個矩陣的一般情況。算法也根據他們是否估計因子矩陣為一個正交矩陣而不同。最後的預測在所有不同最小二乘算法中都是一樣的,但組件是不同的。
擴展
2002年,一個叫做正交投影(英語:Orthogonal Projections to Latent Structures, OPLS)的方法提出。在OPLS中,連續變數數據被分為預測的和不相關的信息。這有利於改進診斷,以及更容易解釋可視化。然而,這些變化只是改善模型的可解釋性,不是生產力。L-PLS通過3個連線數據塊擴展了偏最小二乘回歸。同樣,OPLS-DA(英語:Discriminant Analysis, 判別分析)可能被套用在處理離散變數,如分類和生物標誌物的研究 。
軟體實現
大多數統計軟體包都提供偏最小二乘回歸。R中的‘pls’包提供了一系列算。
