概念
 幾何尺規作圖問題
幾何尺規作圖問題“幾何尺規作圖問題”是指做圖限制只能用直尺、圓規,而這裡的直尺是指沒有刻度只能畫直線的尺。
幾大問題
 幾何尺規作圖問題
幾何尺規作圖問題“幾何尺規作圖問題”包括以下四個問題
1.化圓為方-求作一正方形使其面積等於一已知圓;
2.三等分任意角;
3.倍立方-求作一立方體使其體積是一已知立方體的二倍。
4.做正十七邊形。
問題證明
以上四個問題一直困擾數學家二千多年都不得其解,而實際上這前三大問題都已證明不可能用直尺圓規經有限步驟可解決的。第四個問題是高斯用代數的方法解決的,他也視此為生平得意之作,還交待要把正十七邊形刻在他的墓碑上,但後來他的墓碑上並沒有刻上十七邊形,而是十七角星,因為負責刻碑的雕刻家認為,正十七邊形和圓太像了,大家一定分辨不出來。
解決方法
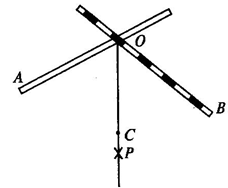
有已知一條線段AB,長a,延長它,用圓規在B點截取兩個等長線段.........。再做出BC垂直AB於B使BC=AB,AC=根號2*a,延長BC至BD,使BD=AC=根號2*a再從點B向AD做垂線,垂足為E,由攝影定理可以求得E是AD的3等分點~再做EF垂直AB於F,點F就是AB的一個3等分點~再做BF的中點就三等分了~可以通過3等分線段來3等分某角..........
以線段的一端為原點,一端為在X軸正方向上建立坐標系。則線段已知相當於兩端點已知,因為知道線段就知道兩端點,知道兩端點就能得出線段。如今要做出X長的線段等價於作兩點距離為X。如今對於已知的兩點我們可以進行如下的操作。1.連線兩點作直線。2.以一點為圓心,與另一點的距離為半徑作圓。3.以一點為圓心,任意距離為半徑作圓。
先講一下什麼叫數域。如果實數集的一個子集有如下性質,任意的元素加減乘除(除數非0)仍在此子集中(叫封閉性),則稱其為某數域。如有有理數域,但沒有整數域(除法不封閉)。重複一下,屬於中兩數四則運算後仍在域內。最小的數域為有理數域。
如今先考慮作圖的1.連線兩點作直線。如果四點坐標皆在某數域中,那么連線兩點得到的兩直線交點也在該數域中。因為A(a1,b1),B(a2,b2),C(a3,b3),D(a4,b4)
都在數域中,則AB,CD方程為(b1-b2)x+(a2-a1)y+(a1b2-a2b1)=0,x,y與常數項係數都是由域中的數四則運算而成,故係數皆在域中。同理直線CD係數也在域中。
這時可求交點,根據加減消元法不難得出交點坐標也在域中。
現在考慮2.以數域中的點為圓心,兩點距離為半徑作圓。圓的方程中的係數都在域內。假設圓與係數在域內某直線相交,則由方程可以得到一點形式為p+q√w的形式,其中p,q,w在域內。於是得到一個擴域。兩域中圓相交情形類似。
3.以任意半徑作圓。任意表示無論取何值作圖一樣成立,於是我們不妨取域中的值,這樣又回到了二。
