概述
最小曼哈頓網路問題復旦大學 2009年6月21日傳來訊息，該校計算機學院大三學生郭澤宇關於最小曼哈頓網路問題的論文被美國ACM學會主辦的第25屆計算幾何國際會議錄用，文章同時作為最佳論文之一被邀請投稿到會議特刊(DCG)。 這意味著計算幾何領域十餘年來未決的重要猜想被這位年僅20歲的本科生成功解決。
背景
最小曼哈頓網路問題，是1999年提出的世界級計算幾何重要猜想。1999年，J. Gudmundsson, C. Levcopoulos和G. Narasimhan最早提出最小曼哈頓網路問題。之後，許多學者研究並給出了這一問題多項式時間近似算法。之前通過組合方法設計的最佳近似算法（3-近似）由M. Benkert等人在2004年給出。2005年，V. Chepoi等人提出了基於線性規劃的2-近似算法，這是目前所知關於這一問題的最好近似度。
2009年6月，被上海復旦大學僅20歲的本科生郭澤宇成功解決。他的關於“最小曼哈頓網路問題”的論文被第25屆計算幾何國際會議錄用，文章同時作為最佳論文之一被邀請投稿到會議特刊Discrete and Computational Geometry(DCG)。
問題
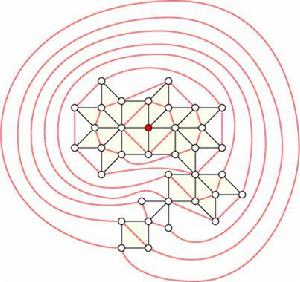最小曼哈頓網路問題給定平面上一個點集T，其Manhattan網路由水平和垂直線段組成，並滿足T中任意兩點間在網路中存在曼哈頓路徑。可知曼哈頓網路即為L1-範數下給定點集的一個1-spanner。更一般的概念稱作geometric spanner或k-spanner，由於具有良好的性質，其套用十分廣泛，包括鄰近問題（proximity problems）的求解、機器人的運動規劃、通信網路的可靠性等等。在本問題中，要求曼哈頓網路中線段總長度最短，即以最小的代價構造給定點集的曼哈頓網路。此外，F. Lam等人在生物序列比對問題中套用了曼哈頓網路的近似算法，顯著減小了搜尋空間。這顯示了最小曼哈頓網路問題在計算生物學中的套用。
解決途徑
設計出具有更優近似度的近似算法
近似算法的設計方法主要包括：局部搜尋，線性規劃方法，原始對偶（primal-dual）方法等。本問題已知的近似算法可以分為兩類：一類方法是將全局最優網路問題規約為局部最優網路問題，再通過局部網路的組合達到全局的較優解，如M. Benkert 等人提出的3-近似算法。在這一方法的使用中，郭澤宇已取得了國際領先的成果。另一類則基於線性規劃方法，如V. Chepoi等人在文獻提出的2-近似算法。
在第一階段的研究中，一方面在已知的最好近似算法基礎上，對問題的性質進行更細緻地分析以嘗試改進；另一方面對近似算法的設計進行系統的學習，探索其他的算法設計思路。
研究問題所屬的複雜性類
儘管在過去的近十年里，最小曼哈頓網路問題受到許多西方計算機科學家的重視，但是到目前為止，人們還不清楚這一問題是否存在多項式時間算法。人們猜想這一問題是NP-完全的，但到目前為止還沒有人給出有效的證明。
一般來講，證明一個問題是NP-完全的基本方式是將一已知的NP完全問題歸約到所研究的問題上。這方面，已知的NP-完全的計算幾何和組合最最佳化問題的歸約過程將具有很大參考價值。例如V. Chepoi在論文中提到的與最小曼哈頓網路問題相當類似的RSA問題，已經由W.Shi 和C. Su給出了從Planar-3-SAT問題到該問題的歸約，從而證明了該問題為NP-完全的。因此，郭澤宇通過閱讀更多的計算幾何學NP-完全問題規約的文章，掌握各種複雜的技巧。試圖給出最小曼哈頓網路問題的類似的歸約方式，從而證明這一問題是NP-完全的。
問題難度
最小曼哈頓網路問題的是否NP-難問題仍屬未知，其不可近似性亦不清楚。因此，研究這一問題所屬的複雜性類將具有極大的理論意義和實際價值。
郭澤宇提出解決最小曼哈頓網路的算法複雜性NP難問題是不太現實的，但改善現有解決方案的效率或提高近似度是可行的研究方向，郭澤宇的結果是2-近似O(n2)時間複雜度。能否將效率提高到O(nlogn)，與3-近似方法相同？或提出1.5-近似的新方法是亟待解決的新問題。
最新進展
復旦大學2009年6月21日傳來訊息，該校計算機學院大三學生郭澤宇關於最小曼哈頓網路問題的論文被美國ACM學會主辦的第25屆計算幾何國際會議錄用，文章同時作為最佳論文之一被邀請投稿到會議特刊(DCG)。
這意味著計算幾何領域十餘年來未決的重要猜想被這位年僅20歲的本科生成功解決。
2008年6月，郭澤宇申請了復旦大學本科生學術研究資助計畫的“莙政”項目。最小曼哈頓網路問題是計算機學院朱洪教授給自己指導的本科生們所開設的題目。
郭澤宇大膽地選擇了這一問題作為項目攻克對象。這既讓朱洪教授和博士研究生孫賀這兩位項目指導老師感到欣喜，也讓“莙政”學者評審專家們捏了一把汗。基於鼓勵本科生創新和支持年輕人闖勁的考慮，郭澤宇最終得到了資助。經過200多個日夜的思考和探索，這一難題終於被他找到突破口。
創新成就
在算法研究領域，人們最重視的是那些長期懸而未決的問題。“曼哈頓網路問題”就是這樣一個不清楚它是否是P還是NP的問題。現在已經有近似度為2的近似算法，但是複雜度為O(n^8)。而郭澤宇把算法改造。使之加快到O(n^2)，是值得讚許的工作。所以被接受為國際會議大會報告，反映了同行對它的重視程度。
曼哈頓網路問題是計算機理論界研究的重要課題，郭澤宇對最小曼哈頓網路的算法複雜性進行研究，有理論意義和套用價值。鑒於目前曼哈頓網路問題是否NP問題尚無明確的結論，目前對曼哈頓網路問題的研究都集中在近似算法的研究。郭澤宇在導師指導下的前期工作對已有的2-近似算法進行改進，使其時間複雜度達到O(n2)(原算法為O(n8))，課題有很好的研究基礎，有望得到進一步的創新成果。
套用方法
郭澤宇怎么解決最小曼哈頓網路問題？
2008年6月，郭澤宇申請了復旦大學本科生學術研究資助計畫的“莙政”項目。最小曼哈頓網路問題是計算機學院朱洪教授給自己指導的本科生們所開設的題目。
郭澤宇大膽地選擇了這一問題作為項目攻克對象。這既讓朱洪教授和博士研究生孫賀這兩位項目指導老師感到欣喜，也讓“莙政”學者評審專家們捏了一把汗。基於鼓勵本科生創新和支持年輕人闖勁的考慮，郭澤宇最終得到了資助。經過200多個日夜的思考和探索，這一難題終於被他找到突破口。
據悉，計算幾何國際會議是計算幾何領域最高級別的會議，這一會議，中國內地數學家已經闊別了整整十八年。
解決歷程
2008年6月，郭澤宇申請了復旦大學本科生學術研究資助計畫的“莙政”項目。最小曼哈頓網路問題是計算機學院朱洪教授給自己指導的本科生們所開設的題目，該課題在城市規劃、網路路由、大規模積體電路設計以及計算生物學等眾多領域有著很好的套用前景。不過自曼哈頓網路的複雜度問題於1999年提出至今，沒有人知道問題的答案，從而使得對這一問題的研究成為計算幾何中最為重要的幾個未解決問題之一。郭澤宇大膽地選擇了這一問題作為項目攻克對象。這既讓朱洪教授和博士研究生孫賀這兩位項目指導老師感到欣喜，也讓“莙政”學者評審專家們捏了一把汗。基於鼓勵本科生創新和支持年輕人闖勁的考慮，郭澤宇最終得到了資助。經過200多個日夜的思考和探索，這一難題終於被他找到突破口。
在郭澤宇的項目申請書中，中國科學院院士陸汝鈐作為推薦老師，對本科生學術研究資助計畫給予了充分的肯定，他認為通過這一方式使許多學生脫穎而出，走上了從事科學研究的道路。記者了解到，1998年，在李政道先生倡導和設立的“莙政基金”支持下，復旦大學開始開展資助優秀本科學生儘早接觸學術研究的計畫，並逐漸形成了一個層次分明、申請時間靈活、申請形式多樣的本科生學術研究資助平台，即復旦大學本科生學術研究資助計畫。
從1998年到2008年，共有1556位學生獲得資助開展研究，其項目學科涵蓋了醫學、工學、理學、文學、教育學等多個領域。另據不完全統計，在2008年，參加復旦大學本科生學術研究資助計畫資助項目的同學在國內外期刊發表論文30篇，其中第一作者文章20篇。
