作圖方法
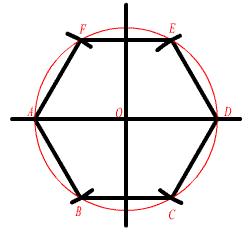
1、正六邊形的畫法
繪製正六邊形,一般利用正六邊形的邊長等於外接圓半徑的原理,繪製步驟如圖所示。
2、正五邊形的畫法
(1)已知正五邊形的邊長AB,繪製正五邊形的方法如圖所示。
①分別以A、B為圓心,AB為半徑畫弧,與AB的中垂線交於K;
②在中垂線上自K向上取CK=2AB/3,得到C點;
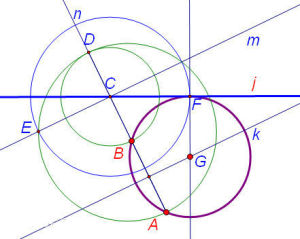
③以C點為圓心,AB為半徑畫圓弧與前面所畫兩段圓弧相交於D、E點,即可得到正五邊形的五個頂點。
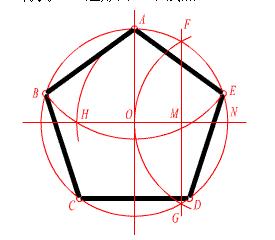
(2)已知外接圓直徑,繪製正五邊形的方法。
①取半徑的中點K;
②以K點為圓心,KA為半徑畫圓弧得到C點;
③AC即為正五邊形邊長,等分圓周得到五個頂點。
①斜度
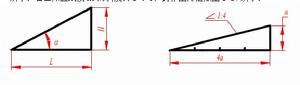
斜度是指一直線或平面對另一直線或平面的傾斜程度。工程上用直角三角形對邊與鄰邊的比值來表示,並固定把比例前項化為1而寫成1:n的形式,如圖1-16(a)所示。若已知直線段AC的斜度為1:5,其作圖方法如圖所示。
②錐度
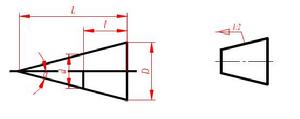
錐度是指圓錐的底圓直徑D與高度H之比,通常,錐度也要寫成1:n的形式。錐度的作圖方法如圖所示。
(4)圓弧連線
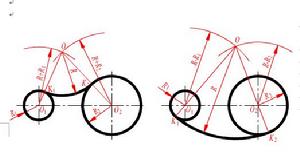
圓弧與圓弧的光滑連線,關鍵在於正確找出連線圓弧的圓心以及切點的位置。由初等幾何知識可知:當兩圓弧以內切方式相連線時,連線弧的圓心要用R-R0來確定;當兩圓弧以外切方式相連線時,連線弧的圓心要用R+R0來確定。用儀器繪圖時,各種圓弧連線的畫法如圖所示。
(a)與兩圓弧外切的畫法;(b)與兩圓弧內切的畫法
(5)橢圓和漸開線的畫法
①橢圓的近似畫法
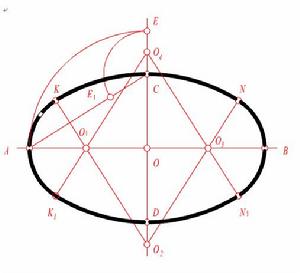
常用的橢圓近似畫法為四圓弧法,即用四段圓弧連線起來的圖形近似代替橢圓。如果已知橢圓的長、短軸AB、CD,則其近似畫法的步驟如下:
a.連AC,以O為圓心,OA為半徑畫弧交CD延長線於E,再以C為圓心,CE為半徑畫弧交AC於F;
b.作AF線段的中垂線分別交長、短軸於O1、O2,並作O1、O2的對稱點O3、O4,即求出四段圓弧的圓心,如圖所示。
②漸開線的近似畫法
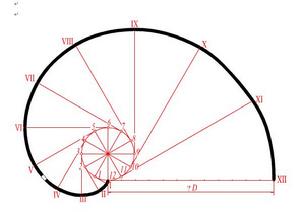
直線在圓周上作無滑動的滾動,該直線上一點的軌跡即為此圓(稱作基圓)的漸開線。齒輪的齒廓曲線大都是漸開線,如圖1-21所示。
其作圖步驟如下:
a.畫基圓並將其圓周n等分(圖1-21中,n=12);
b.將基圓周的展開長度πD也分成相同等分;
c.過基圓上各等分點按同一方向作基圓的切線;
d.依次在各切線上量取1/nπD、2/nπD…、πD,得到基圓的漸開線。
工具使用
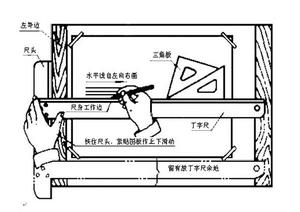
1、圖板
圖板是供鋪放圖紙用的空心木板,表面須經磨平磨光,左右兩導邊要平直,繪圖時用膠帶紙將圖紙固定在圖板的適當位置上。
2、丁字尺
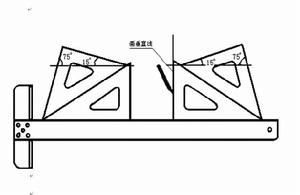
丁字尺由尺頭和尺身組成。尺頭較短,固定在尺身的左端,其內側邊與尺身上方的工作邊垂直。當尺頭的內側邊貼緊圖板的左導邊時,即沿尺身的工作邊畫出水平線。讓其緊貼圖板導邊上下移動,則可畫出不同位置的水平線。丁字尺還可同三角板配合使用。3、三角板三角板由一塊45°的等腰直角三角形和一塊30°、60°的直角三角形組成,它們與丁字尺配合使用可劃出垂直線和15°整倍數的斜線。兩塊三角板配合可畫出任意斜線、水平線和垂直線。
4、鉛筆
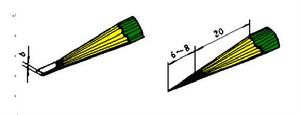
繪圖鉛筆的鉛芯有軟硬之分,軟(B)、硬(H)、中性(HB)三種。一般2H、3H畫細線,H寫字畫箭頭。這些鉛筆都應削成較長鉛芯且磨成錐狀。HB或B用於畫粗實線,鉛芯較短,削磨成四稜柱形,以保證畫出粗實線均勻一致。
分規用來量取線段、等分線段和截取尺寸等。分規兩腿端部有鋼針,當合攏兩腿時兩針尖應匯交於一點。

圓規用於畫圓弧和圓,它的固定腿上裝有鋼針,鋼針的兩端形狀不同,帶有台階的一端用於畫圓和圓弧,使用時將針尖全部扎入圖板,台階接觸紙面,具有肘關節的腿用來插鉛筆或直線筆的插腿,畫圓時要彎曲肘關節並調整針尖方向,使它們分別垂直於紙面。畫大圖時要加延長桿。
三大問題
1.化圓為方-求作一正方形使其面積等於一已知圓;
2.三等分任意角;
3.倍立方-求作一立方體使其體積是一已知立方體的二倍。
圓與正方形都是常見的幾何圖形,但如何作一個正方形和已知圓等面積呢?若已知圓的半徑為1則其面積為π(1)2=π,所以化圓為方的問題等於去求一正方形其面積為π,也就是用尺規做出長度為π1/2的線段(或者是π的線段)。
三大問題的第二個是三等分一個角的問題。對於某些角如90。、180。三等分並不難,但是否所有角都可以三等分呢?例如60。,若能三等分則可以做出20。的角,那么正18邊形及正九邊形也都可以做出來了(註:圓內接一正十八邊形每一邊所對的圓周角為360。/18=20。)。其實三等分角的問題是由求作正多邊形這一類問題所引起來的。
第三個問題是倍立方。埃拉托塞尼(公元前276年~公元前195年)曾經記述一個神話提到說有一個先知者得到神諭必須將立方形的祭壇的體積加倍,有人主張將每邊長加倍,但我們都知道那是錯誤的,因為體積已經變成原來的8倍。這些問題困擾數學家一千多年都不得其解,而實際上這三大問題都不可能用直尺圓規經有限步驟可解決的。