![數論[數學分支]](/img/3/bca/nBnauM3XwIjM0ADO0QTM5EDN0UTMyITNykTO0EDMwAjMwUzL0EzLyUzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg "數論[數學分支]")
簡介
數學理論或在較舊的使用中，叫做算術，是專門研究整數的純數學的分支。它有時被稱為“數學女王”，因為它在原理中的基礎地位。數理論家研究質數以及由整數（例如有理數字）製成的對象的屬性或定義為整數的概括（例如，代數整數）。
整數可以自己考慮或作為方程（Diophantine幾何）的解決方案。通過研究以某種方式（分析數論）編碼整數，素數或其他數論理論對象的分析對象（如Riemann zeta函式），通常最好地理解數論中的問題。人們還可以研究與有理數相關的實數，例如，由後者近似（Diophantine近似）。
數理論的較舊術語是算術。到二十世紀初，它被“數學理論”所取代（“算術”一詞被普通大眾用來表示“基本計算”，也在數學邏輯中獲得了其他含義，如在數學理論中使用術語算術在二十世紀下半葉重新獲得了一些地位，這可能部分是由於法國的影響力，特別是作為數理論的形容詞，優選算術。
發展歷史
古希臘數學家——歐幾里得數論早期稱為算術。到20世紀初，才開始使用數論的名稱，而算術一詞則表示“基本運算”，不過在20世紀的後半，有部份數學家仍會用“算術”一詞來表示數論。1952年時數學家Harold Davenport仍用“高等算術”一詞來表示數論，戈弗雷·哈羅德·哈代和愛德華·梅特蘭·賴特在1938年寫《數論介紹》簡介時曾提到“我們曾考慮過將書名改為《算術介紹》，某方面而言是更合適的書名，但也容易讓讀者誤會其中的內容”。
公元前300年，古希臘數學家歐幾里德證明了有無窮多個素數，公元前250年古希臘數學家埃拉托塞尼發明了一種尋找素數的埃拉托斯特尼篩法。尋找一個表示所有素數的素數通項公式，或者叫素數普遍公式，是古典數論最主要的問題之一。
數論從早期到中期跨越了1000—2000年，在接近2000年時間，數論幾乎是空白。中期主要指15-16世紀到19世紀，是由費馬，梅森、歐拉、高斯、勒讓德、黎曼、希爾伯特、Heegner等人發展的。
內容是尋找素數通項公式為主線的思想，開始由初等數論向解析數論和代數數論轉變，產生了越來越多的猜想無法解決，遺留到20世紀，許許多多的困難還是依賴素數通項公式，例如黎曼猜想。如果找到一個素數通項公式，一些困難問題就可以由解析數論轉回到初等數論範圍。
到了十八世紀末，歷代數學家積累的關於整數性質零散的知識已經十分豐富了，但是仍然沒有找到素數產生的模式。德國數學家高斯集中前人的大成，寫了一本書叫做《算術研究》，1800年寄給了法國科學院，但是法國科學院拒絕了高斯的這部傑作，高斯只好在1801年自己發表了這部著作。這部書開始了現代數論的新紀元。在《算術研究》中，高斯把過去研究整數性質所用的符號標準化了，把當時現存的定理系統化並進行了推廣，把要研究的問題和已知的方法進行了分類，還引進了新的方法。高斯在這一著作中主要提出了同餘理論， 並發現了著名的二次互反律， 被其譽之為“數論之酵母”。
黎曼在研究ζ函式時，發現了複變函數的解析性質和素數分布之間的深刻聯繫， 由此將數論領進了分析的領域。這方面主要的代表人物還有英國著名數論學家哈代、李特伍德、拉馬努金等等。在國內，則有華羅庚、陳景潤、王元等等。
另一方面， 由於此前人們一直關注費馬大定理的證明， 所以又發展出了代數數論的研究課題。比如庫默爾提出了理想數的概念--可惜他當時忽略了代數擴環的唯一分解定理不一定成立）。高斯研究了復整數環的理論--即高斯整數。他在3次情形的費馬猜想中也用了擴環的代數數論性質。代數數論發展的一個里程碑，則是希爾伯特的《數論報告》。
隨著數學工具的不斷深化， 數論開始和代數幾何深刻聯繫起來， 最終發展稱為當今最深刻的數學理論，諸如算術代數幾何， 它們將許多此前的研究方法和研究觀點最終統一起來， 從更加高的觀點出發，進行研究和探討。
由於近代計算機科學和套用數學的發展，數論得到了廣泛的套用。比如在計算方法、代數編碼、組合論等方面都廣泛使用了初等數論範圍內的許多研究成果；又文獻報導，有些國家套用“孫子定理”來進行測距，用原根和指數來計算離散傅立葉變換等。此外，數論的許多比較深刻的研究成果也在近似分析、差集合、快速變換等方面得到了套用。特別是由於計算機的發展，用離散量的計算去逼近連續量而達到所要求的精度已成為可能。
門類
初等數論
高斯於其著作《算術研究》探討了二次互反律初等數論主要就是研究整數環的整除理論及同餘理論。此外它也包括了連分數理論和少許不定方程的問題。本質上說，初等數論的研究手段局限在整除性質上。
初等數論中經典的結論包括算術基本定理、歐幾里得的質數無限證明、中國剩餘定理、歐拉定理（其特例是費馬小定理）、高斯的二次互反律， 勾股方程的商高定理、佩爾方程的連分數求解法等等。
解析數論
藉助微積分及複分析（即複變函數）來研究關於整數的問題，主要又可以分為乘性數論與加性數論兩類。乘性數論藉由研究積性生成函式的性質來探討素數分布的問題，其中質數定理與狄利克雷定理為這個領域中最著名的古典成果。加性數論則是研究整數的加法分解之可能性與表示的問題，華林問題是該領域最著名的課題。
解析數論的創立當歸功於黎曼。他發現了黎曼zeta函式之解析性質與數論中的素數分布問題存在深刻聯繫。確切的說， 黎曼ζ函式的非平凡零點的分布情況決定了素數的很多性質。黎曼猜測， 那些零點都落在複平面上實部為1/2的直線上。這就是著名的黎曼假設—千禧年大獎難題之一。值得注意的是， 歐拉實際上在處理素數無限問題時也用到了解析方法。
解析數論方法除了圓法、篩法等等之外， 也包括和橢圓曲線相關的模形式理論等等。此後又發展到自守形式理論，從而和表示論聯繫起來。
代數數論
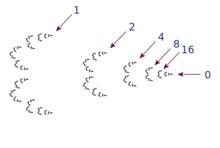2進數里的整數，詳見代數數論，將整數環的數論性質研究擴展到了更一般的整環上，特別是代數數域。一個主要課題就是關於代數整數的研究，目標是為了更一般地解決不定方程求解的問題。其中一個主要的歷史動力來自於尋找費馬大定理的證明。
代數數論更傾向於從代數結構角度去研究各類整環的性質， 比如在給定整環上是否存在算術基本定理等等。
這個領域與代數幾何之間的關聯尤其緊密， 它實際上也構成了交換代數理論的一部分。它也包括了其他深刻內容，比如表示論、p-adic理論等等。
幾何數論
主要在於通過幾何觀點研究整數（在此即格點， 也稱整點）的分布情形。最著名的定理為Minkowski定理。這門理論也是有閔科夫斯基所創。對於研究二次型理論有著重要作用。
計算數論
藉助電腦的算法幫助研究數論的問題，例如素數測試和因數分解等和密碼學息息相關的課題。
超越數論
研究數的超越性，其中對於歐拉常數與特定的riemann ζ函式值之研究尤其令人感到興趣。此外它也探討了數的丟番圖逼近理論。
組合數論
利用組合和機率的技巧，非構造性地證明某些無法用初等方式處理的複雜結論。這是由保羅·艾狄胥開創的思路。比如蘭伯特猜想的簡化證明。
算術代數幾何
這是數論發展到目前為止最深刻最前沿的領域， 可謂集大成者。它從代數幾何的觀點出發，通過深刻的數學工具去研究數論的性質。比如懷爾斯證明費馬猜想就是這方面的經典實例。整個證明幾乎用到了當時所有最深刻的理論工具。
當代數論的一個重要的研究指導綱領，就是著名的郎蘭茲綱領。
研究方法
除了上述傳統方法之外，也有其他一些研究數論之法， 但是沒有完全得到數學家的認可。比如有物理學家，通過量子力學方法聲稱證明了黎曼假設。
猜想
●哥德巴赫猜想：是否每個大於2的偶數都可寫成兩個質數之和？
●孿生素數猜想：孿生素數就是差為2的素數對，例如11和13。是否存在無窮多的孿生素數？
●斐波那契數列內是否存在無窮多的素數？
●是否存在無窮多的梅森素數？（指形如2 －1的正整數，其中指數p是素數，常記為M 。若M是素數，則稱為梅森素數）
●1995年懷爾斯和理查·泰勒證明了歷時350年的費馬猜想（費馬大定理）。
●黎曼猜想
進展
數論是純粹數學的分支之一，主要研究整數的性質。而整數的基本元素是素數（也稱質數），所以數論的本質是對素數性質的研究。數論被高斯譽為“數學中的皇冠”。因此，數學家都喜歡把數論中一些懸而未決的疑難問題，叫做“皇冠上的明珠”，以鼓勵人們去“摘取”。近年以來數論研究獲得了多項突破性 進展，這讓數學界感到萬分驚喜。
發現已知的最大素數
美國中央密蘇里大學數學家柯蒂斯·庫珀領導的研究小組通過參加一個名為“網際網路梅森素數大搜尋”（GIMPS）的國際合作項目，於1月25日發現了目前已知的最大素數——2^57885161-1 （即2的57885161次方減1）。該素數是第48個梅森素數，有17425170位；如果用普通字號將它連續列印下來，其長度可超過65公里！美國數學學會發言人邁克·布林宣稱：這是 數論研究的一項重大突破。
研究小組在大約1000台大學裡的計算機上運行GIMPS的軟體，每台計算機都不間斷地用了39天時間證明257885161-1是個素數。之後其他研究者也獨立驗證了這一結果。近年來，庫珀通過參加GIMPS項目一共發現了3個梅森素數。
尋找梅森素數已成為發現已知最大素數的最有效途徑。如今世界上有180多個國家和地區近28萬人參加了GIMPS項目，並動用超過79萬台計算機聯網來尋找新的梅森素數。梅森素數是否有無窮多個？這是一個尚未破解的著名數學謎題。
證明“弱孿生素數猜想”
美國新罕布夏大學數學家張益唐經過多年努力，在不依賴未經證明推論的前提下，率先證明了一個“弱孿生素數猜想”，即“存在無窮多個之差小於7000萬的素數對”。4月17日，他將論文投稿給世界頂級期刊《數學年刊》。美國數學家、審稿人之一亨里克·艾溫尼科評價說：“這是一流的數學工作。”他相信不久會有很多人把“7000萬”這個數字“變小”。
儘管從證明弱孿生素數猜想到證明孿生素數猜想還有相當的距離，英國《自然》雜誌線上報導還是稱張益唐的證明為一個“重要的里程碑”。由於孿生素數猜想與哥德巴赫猜想密切相關（姐妹問題），很多數學家希望通過解決這個猜想，進而攻克哥德巴赫猜想。
值得一提的是，英國數學家戈弗雷·哈代和約翰·李特爾伍德曾提出一個“強孿生素數猜想”。這一猜想不僅提出孿生素數有無窮多對，而且還給出其漸近分布形式。中國數學家周海中指出：要證明強孿生素數猜想，人們仍要面對許多巨大的困難。
解開“弱哥德巴赫猜想”
5月13日，秘魯數學家哈拉爾德·赫爾弗戈特在巴黎高等師範學院宣稱：證明了一個“弱哥德巴赫猜想”，即“任何一個大於7的奇數都能被表示成3個奇素數之和”。他將論文投稿給全球最大的預印本網站（arXiv）；有專家認為這是哥德巴赫猜想研究的一項重大成果。不過，其證明是否成立，還有待進一步考證。
赫爾弗戈特在論證技術上主要使用了哈代-李特爾伍德-維諾格拉多夫圓法。在這一圓法中，數學家創建了一個周期函式，其範圍包括所有素數。1923年，哈代和李特爾伍德證明，假設廣義黎曼猜想成立，三元哥德巴赫猜想對充分大的奇數是正確的；1937年，蘇聯數學家伊萬·維諾格拉多夫更進一步，在無須廣義黎曼猜想的情形下，直接證明了充分大的奇數可以表示為3個素數之和。
英國數學家安德魯·格蘭維爾稱，不幸的是，由於技術原因，赫爾弗戈特的方法很難證明“強哥德巴赫猜想”，即“關於偶數的哥德巴赫猜想”。如今數學界的主流意見認為：要證明強哥德巴赫猜想，還需要新的思路和工具，或者在現有的方法上進行重大的改進 。（鄭輝 作者系新加坡南洋理工大學教授 ）
我國的數論發展
在我國近代，數論也是發展最早的數學分支之一。從二十世紀三十年代開始，在解析數論、丟番圖方程、一致分布等方面都有過重要的貢獻，出現了華羅庚、閔嗣鶴、柯召、陳景潤、潘承洞等第一流的數論專家。其中華羅庚教授在三角和估值、堆砌素數論方面的研究是享有盛名的。1949年以後，數論的研究的得到了更大的發展。陳景潤、王元等在“篩法”和“哥德巴赫猜想”方面的研究，已取得世界領先的優秀成績；周海中在著名數論難題——梅森素數分布的研究中取得了世界領先的卓著成績。
