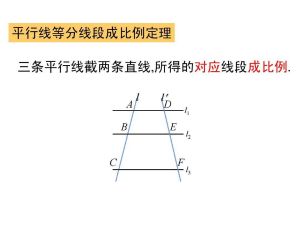
定理內容
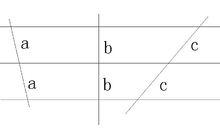附圖如果一組等距的平行線在一條直線上截得的線段相等，那么在其他直線上截得的線段也相等
經過三角形一邊中點且與另一邊平行的直線必平分第三邊
經過梯形一腰的中點且與底邊平行的直線必平分另一腰
第二條定理也做：三角形過一邊中點的直線平行第二邊平分第三邊。 也稱“一二三定理”。
第二第三條即常說的“中位線定理”。
證明過程
證明如下：
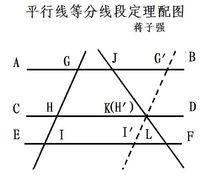
已知：AB∥CD∥EF,GI,JL交AB,CD,EF於點G,J,H,K,I,L.（如右圖)
求證：GH:HI=JK:KL
平行線等分線段定理證明：過點K作G'I'∥GI交AB ,CD ,EF於點G',H' I'.
∵ AB∥CD∥EF,G'I'∥GI
∴ 四邊形GHKG',HII'H‘,GII'G是平行四邊形（平行四邊形判定定理），∠BJK=∠KLI,∠JG'I'=∠G'I'F（內錯角相等）
∴△JG'K∽△I'LK,（相似三角形判定），GH=G'H',HI=H'I'（平行四邊形對邊相等）
∵G'H':H'I'=JK:KL(相似三角形性質）
∴GH:HI=JK:KL（等量代換）
推論1：過三角形一邊中點與另一邊平行的直線必平分第三邊
推論2：過梯形一腰中點且平行於底邊的直線必過另一腰中點
