幾何度量
正文
在D.希爾伯特建立的歐幾里得幾何的公理體系（見歐幾里得幾何學)的基礎上,線段度量的理論安排在連續公理之後，是以結合公理、順序公理、契約公理、連續公理等四組公理為理論基礎而進行論述的。關於線段的長度是這樣定義的：對應於線段AB，且具有下列性質的正數，叫做線段AB 的長度，記作ρ(AB)。
① 與相等的線段對應的是相等的正數,即如果線段
AB=A′B′，
那么ρ(AB)=ρ(A′B′)。
② 如果B是線段AC上一點，對應於線段AB和BC的正數的和必等於對應於AC 的正數。即ρ(AB)+ρ(BC)=ρ(AC)。
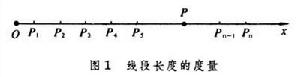
由此定義出發可以證明，作為線段長度的正數是存在的；當選定了單位長度,也就是選定了對應於正數1的線段後，作為每一線段長度的正數是惟一的。而且還明確了, 如果在射線Ox上順次截取線段OP1=P1P2＝P2P3＝…＝Pn-1Pn＝…,且ρ(OP1) = 1時，ρ(OP2)、ρ(OP3)、…、ρ(OPn) 、… 必須且僅須順次為2、3、…、n、…（圖1
）。 以連續公理中的阿基米德公理為主要論據，可以證明,選定了ρ(OP1)=1之後,對應於射線上任意線段OP，必有且僅有一個正實數k存在，使得ρ(OP)=k。
以連續公理中的康托爾公理為主要論據，可以證明，選定了ρ(OP1)=1之後，對應於給定的正實數k,射線Ox上必有且僅有一點P存在，使得ρ(OP)=k。
關於角的度量問題的論述，均仿此。
關於簡單多邊形的面積的定義是：
對應於一個簡單多邊形,且具有下列性質的正數,叫做這個多邊形的面積。
① 與契約的多邊形對應的是相等的正數。
② 兩多邊形之和的面積等於兩多邊形面積的和。
如果以長度單位為一邊的正方形為面積單位，那么邊長為有理數的矩形的面積就是它能分割成面積單位的個數，因而等於兩邊長度之積。對邊長為無理數的矩形的面積，可在此基礎上用極限來解決，其理論如下：
設矩形ABCD的邊長AB、BC 都是無理數,以長度單位度量BA和BC,分別量至BA1、BA2(BA1<BA<BA2)；BC1、BC2(BC1<BC<BC2)（圖2
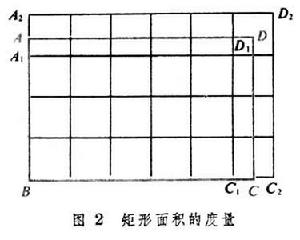）。 分別以BA1和BC1、BA2和BC2為邊完成矩形A1BC1D1和A2BC2D2，設矩形A1BC1D1和A2BC2D2分別分割為m和m＋n個面積單位（設為u）。那么
mu<ABCD<(m+n)u。
如果以長度單位
（不失一般性設為 
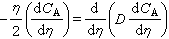）為一邊完成正方形 u′,則
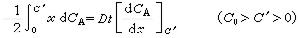。而以該單位長度的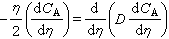度量BA和BC，分別量至BA姈和BA娦,即BA姈<BA<BA娦；BC姈和BC娦,即BC姈<BC<BC娦 (圖中沒畫出)；且以BA姈和BC姈、BA娦和BC娦完成矩形 A姈BC姈D姈和A娦BC娦D娦，並設兩矩形分別分割為m1和m1+n1個u′，即
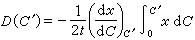和
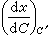那么 <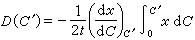
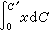
仿此，依原長度單位的
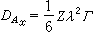順次進行，連同所得兩不等式，便得到： m·u<ABCD<(m+n)·u，
…………。
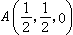
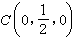
為一無窮遞增數列；而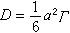
為一無窮遞縮數列。它們相當項之差為：
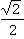此數列的極限為0。因而前兩數列有相同的極限。這樣，就以此極限定義為矩形的面積。依此可證矩形的面積等於其兩鄰邊長度之積。 關於圓周長度與圓面積，在初等幾何中是這樣來定義的:由於一個圓的內接正n邊形和外切正n邊形,當邊數無限倍增時，一系列的內接正多邊形的周的長度構成一無窮遞增數列，一系列的外切正多邊形的周的長度構成一無窮遞縮數列，這兩數列有相同的極限。這樣，就以此極限定義為圓周長度。
同樣，兩系列的多邊形的面積也分別構成一無窮遞增數列和一無窮遞縮數列。這兩數列也有相同極限。這樣，就以此極限定義為圓的面積。
根據上述定義，可證明圓周長度C=2πr；圓面積S =πr2，式中r為圓的半徑；π為圓周率。
關於簡單多面體體積的論述，均仿簡單多邊形面積的論述。
關於球的表面積和體積的論述，均仿圓周長度和面積的論述。
