對數:對數是中學初等數學中的重要內容，是一種計算特殊多位數之間乘積的方法 -百科知識中文網

歷史

16、17世紀之交，隨著天文、航海、工程、貿易以及軍事的發展，改進數字計算方法成了當務之急。納皮爾（J.Napier，1550—1617）正是在研究天文學的過程中，為了簡化其中的計算而發明了對數.對數的發明是數學史上的重大事件，天文學界更是以近乎狂喜的心情迎接這一發明。恩格斯曾經把對數的發明和解析幾何的創始、微積分的建立稱為17世紀數學的三大成就，伽利略也說過：“給我空間、時間及對數，我就可以創造一個宇宙。”

對數發明之前，人們對三角運算中將三角函式的積化為三角函式的和或差的方法已很熟悉，而且德國數學家斯蒂弗爾（M.Stifel，約1487—1567）在《綜合算術》（1544年）中闡述了一種如下所示的一種對應關係：

該關係可被歸納為，同時該種關係之間存在的運算性質（即上面一行數字的乘、除、乘方、開方對應於下面一行數字的加、減、乘、除）也已廣為人知。經過對運算體系的多年研究，納皮爾在1614年出版了《奇妙的對數定律說明書》，書中藉助運動學，用幾何術語闡述了對數方法。

將對數加以改造使之廣泛流傳的是納皮爾的朋友布里格斯（H.Briggs，1561—1631），他通過研究《奇妙的對數定律說明書》，感到其中的對數用起來很不方便，於是與納皮爾商定，使1的對數為0，10的對數為1，這樣就得到了以10為底的常用對數。由於我們的數系是十進制，因此它在數值上計算具有優越性。1624年，布里格斯出版了《對數算術》，公布了以10為底包含1~20000及90000~100000的14位常用對數表。

根據對數運算原理，人們還發明了對數計算尺。300多年來，對數計算尺一直是科學工作者，特別是工程技術人員必備的計算工具，直到20世紀70年代才讓位給電子計算器。儘管作為一種計算工具，對數計算尺、對數表都不再重要了，但是，對數的思想方法卻仍然具有生命力。

從對數的發明過程我們可以發現，納皮爾在討論對數概念時，並沒有使用指數與對數的互逆關係，造成這種狀況的主要原因是當時還沒有明確的指數概念，就連指數符號也是在20多年後的1637年才由法國數學家笛卡兒（R.Descartes，1596—1650）開始使用。直到18世紀，才由瑞士數學家歐拉發現了指數與對數的互逆關係。在1770年出版的一部著作中，歐拉首先使用來定義，他指出：“對數源於指數”。對數的發明先於指數，成為數學史上的珍聞。

從對數的發明過程可以看到，社會生產、科學技術的需要是數學發展的主要動力。建立對數與指數之間的聯繫的過程表明，使用較好的符號體系對於數學的發展是至關重要的。實際上，好的數學符號能夠大大地節省人的思維負擔。數學家們對數學符號體系的發展與完善作出了長期而艱苦的努力。

符號

以a為底N的對數記作。對數符號log出自拉丁文logarithm，最早由義大利數學家卡瓦列里（Cavalieri）所使用。20世紀初，形成了對數的現代表示。為了使用方便，人們逐漸把以10為底的常用對數及以無理數e為底的自然對數分別記作lgN和lnN。

定義

如果

，即a的x次方等於N（a>0，且a≠1），那么數x叫做以a為底N的對數（logarithm），記作

。其中，a叫做對數的底數，N叫做真數，x叫做“以a為底N的對數”。
1、特別地，我們稱以10為底的對數叫做常用對數（common logarithm），並記為lg。

2、稱以無理數e（e=2.71828...）為底的對數稱為自然對數（natural logarithm），並記為ln。

3、零沒有對數。

4、在實數範圍內，負數無對數。在複數範圍內，負數是有對數的。
事實上，當，，則有e（2k+1）πi+1=0，所以ln(-1)的具有周期性的多個值，ln（-1）=（2k+1）πi。這樣，任意一個負數的自然對數都具有周期性的多個值。例如：ln（-5）=（2k+1）πi+ln5。

方程式

基本公式

證明過程

對數函式

定義

函式

叫做對數函式（logarithmic function），其中x是自變數。對數函式的定義域是

。函式基本性質1、過定點

，即x=1時，y=0。2、當

時，在

上是減函式；當

時，在

上是增函式。

複變函數

，e是自然對數的底，i是虛數單位。它將指數函式的定義域擴大到複數，建立了三角函式和指數函式的關係，它在複變函數論里占有非常重要的地位，被譽為“數學中的天橋”。

的推導：因為

在

的展開式中把x換成±ix.

所以

將公式里的x換成-x，得到：

，然後採用兩式相加減的方法得到：

，

.這兩個也叫做歐拉公式。將

中的x取作π就得到：

這個恆等式也叫做歐拉公式，它是數學裡最令人著迷的一個公式，它將數學裡最重要的幾個數字聯繫到了一起：兩個超越數：自然對數的底e ，圓周率π，兩個單位：虛數單位i和自然數的單位1，以及被稱為人類偉大發現之一的0。數學家們評價它是“上帝創造的公式”。

函式圖象

1.對數函式的圖象都過（1,0）點.

2.對於y=log(a)(n)函式,

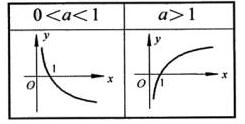
①,當0<1時,圖象上函式顯示為(0,+∞)單減.隨著a 的增大,圖象逐漸以(1,0)點為軸順時針轉動,但不超過X=1.

②當a>1時,圖象上顯示函式為(0,+∞)單增,隨著a的增大,圖象逐漸以(1.0)點為軸逆時針轉動,但不超過X=1.

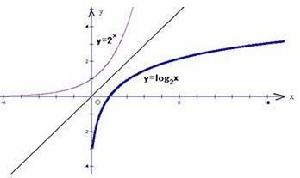
3.與其他函式與反函式之間圖象關係相同,對數函式和指數函式的圖象關於直線y=x對稱。

數據表

100以內對數表

log	0	1	2	3	4	5	6	7	8	9
10	0000	0043	0086	0128	0170	0212	0253	0294	0334	0374
11	0414	0453	0492	0531	0569	0607	0645	0682	0719	0755
12	0792	0828	0864	0899	0934	0969	1004	1038	1072	1106
13	1139	1173	1206	1239	1271	1303	1335	1367	1399	1430
14	1461	1492	1523	1553	1584	1614	1644	1673	1703	1732
15	1761	1790	1818	1847	1875	1903	1931	1959	1987	2014
16	2041	2068	2095	2122	2148	2175	2201	2227	2253	2279
17	2304	2330	2355	2380	2405	2430	2455	2480	2504	2529
18	2553	2577	2601	2625	2648	2672	2695	2718	2742	2765
19	2788	2810	2833	2856	2878	2900	2923	2945	2967	2989
20	3010	3032	3054	3075	3096	3118	3139	3160	3181	3201
21	3222	3243	3263	3284	3304	3324	3345	3365	3385	3404
22	3424	3444	3464	3483	3502	3522	3541	3560	3579	3598
23	3617	3636	3655	3674	3692	3711	3729	3747	3766	3784
24	3802	3820	3838	3856	3874	3892	3909	3927	3945	3962
25	3979	3997	4014	4031	4048	4065	4082	4099	4116	4133
26	4150	4166	4183	4200	4216	4232	4249	4265	4281	4298
27	4314	4330	4346	4362	4378	4393	4409	4425	4440	4456
28	4472	4487	4502	4518	4533	4548	4564	4579	4594	4609
29	4624	4639	4654	4669	4683	4698	4713	4728	4742	4757
30	4771	4786	4800	4814	4829	4843	4857	4871	4886	4900
31	4914	4928	4942	4955	4969	4983	4997	5011	5024	5038
32	5051	5065	5079	5092	5105	5119	5132	5145	5159	5172
33	5185	5198	5211	5224	5237	5250	5263	5276	5289	5302
34	5315	5328	5340	5353	5366	5378	5391	5403	5416	5428
35	5441	5453	5465	5478	5490	5502	5514	5527	5539	5551
36	5563	5575	5587	5599	5611	5623	5635	5647	5658	5670
37	5682	5694	5705	5717	5729	5740	5752	5763	5775	5786
38	5798	5809	5821	5832	5843	5855	5866	5877	5888	5899
39	5911	5922	5933	5944	5955	5966	5977	5988	5999	6010
40	6021	6031	6042	6053	6064	6075	6085	6096	6107	6117
41	6128	6138	6149	6160	6170	6180	6191	6201	6212	6222
42	6232	6243	6253	6263	6274	6284	6294	6304	6314	6325
43	6335	6345	6355	6365	6375	6385	6395	6405	6415	6425
44	6435	6444	6454	6464	6474	6484	6493	6503	6513	6522
45	6532	6542	6551	6561	6571	6580	6590	6599	6609	6618
46	6628	6637	6646	6656	6665	6675	6684	6693	6702	6712
47	6721	6730	6739	6749	6758	6767	6776	6785	6794	6803
48	6812	6821	6830	6839	6848	6857	6866	6875	6884	6893
49	6902	6911	6920	6928	6937	6946	6955	6964	6972	6981
50	6990	6998	7007	7016	7024	7033	7042	7050	7059	7067
51	7076	7084	7093	7101	7110	7118	7126	7135	7143	7152
52	7160	7168	7177	7185	7193	7202	7210	7218	7226	7235
53	7243	7251	7259	7267	7275	7284	7292	7300	7308	7316
54	7324	7332	7340	7348	7356	7364	7372	7380	7388	7396
55	7404	7412	7419	7427	7435	7443	7451	7459	7466	7474
56	7482	7490	7497	7505	7513	7520	7528	7536	7543	7551
57	7559	7566	7574	7582	7589	7597	7604	7612	7619	7627
58	7634	7642	7649	7657	7664	7672	7679	7686	7694	7701
59	7709	7716	7723	7731	7738	7745	7752	7760	7767	7774
60	7782	7789	7796	7803	7810	7818	7825	7832	7839	7846
61	7853	7860	7868	7875	7882	7889	7896	7903	7910	7917
62	7924	7931	7938	7945	7952	7959	7966	7973	7980	7987
63	7993	8000	8007	8014	8021	8028	8035	8041	8048	8055
64	8062	8069	8075	8082	8089	8096	8102	8109	8116	8122
65	8129	8136	8142	8149	8156	8162	8169	8176	8182	8189
66	8195	8202	8209	8215	8222	8228	8235	8241	8248	8254
67	8261	8267	8274	8280	8287	8293	8299	8306	8312	8319
68	8325	8331	8338	8344	8351	8357	8363	8370	8376	8382
69	8388	8395	8401	8407	8414	8420	8426	8432	8439	8445
70	8451	8457	8463	8470	8476	8482	8488	8494	8500	8506
71	8513	8519	8525	8531	8537	8543	8549	8555	8561	8567
72	8573	8579	8585	8591	8597	8603	8609	8615	8621	8627
73	8633	8639	8645	8651	8657	8663	8669	8675	8681	8686
74	8692	8698	8704	8710	8716	8722	8727	8733	8739	8745
75	8751	8756	8762	8768	8774	8779	8785	8791	8797	8802
76	8808	8814	8820	8825	8831	8837	8842	8848	8854	8859
77	8865	8871	8876	8882	8887	8893	8899	8904	8910	8915
78	8921	8927	8932	8938	8943	8949	8954	8960	8965	8971
79	8976	8982	8987	8993	8998	9004	9009	9015	9020	9025
80	9031	9036	9042	9047	9053	9058	9063	9069	9074	9079
81	9085	9090	9096	9101	9106	9112	9117	9122	9128	9133
82	9138	9143	9149	9154	9159	9165	9170	9175	9180	9186
83	9191	9196	9201	9206	9212	9217	9222	9227	9232	9238
84	9243	9248	9253	9258	9263	9269	9274	9279	9284	9289
85	9294	9299	9304	9309	9315	9320	9325	9330	9335	9340
86	9345	9350	9355	9360	9365	9370	9375	9380	9385	9390
87	9395	9400	9405	9410	9415	9420	9425	9430	9435	9440
88	9445	9450	9455	9460	9465	9469	9474	9479	9484	9489
89	9494	9499	9504	9509	9513	9518	9523	9528	9533	9538
90	9542	9547	9552	9557	9562	9566	9571	9576	9581	9586
91	9590	9595	9600	9605	9609	9614	9619	9624	9628	9633
92	9638	9643	9647	9652	9657	9661	9666	9671	9675	9680
93	9685	9689	9694	9699	9703	9708	9713	9717	9722	9727
94	9731	9736	9741	9745	9750	9754	9759	9763	9768	9773
95	9777	9782	9786	9791	9795	9800	9805	9809	9814	9818
96	9823	9827	9832	9836	9841	9845	9850	9854	9859	9863
97	9868	9872	9877	9881	9886	9890	9894	9899	9903	9908
98	9912	9917	9921	9926	9930	9934	9939	9943	9948	9952
99	9956	9961	9965	9969	9974	9978	9983	9987	9991	9996

對數

基本信息

歷史

符號

定義

方程式

基本公式

證明過程

對數函式

複變函數

函式圖象

數據表

相關詞條

反對數

半對數坐標

半對數線圖

離散對數

對數螺線

對數曲線

對數維

對數坐標

相關搜尋

熱門詞條