性質
基本知識
 對數公式
對數公式① ;
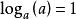 對數公式
對數公式② ;
③負數與零無對數.
 對數公式
對數公式 對數公式
對數公式④ * =1;
恆等式及證明
 對數公式運算的理解與推導by尋韻天下
對數公式運算的理解與推導by尋韻天下a^log(a)(N)=N (a>0 ,a≠1) 推導:log(a) (a^N)=N恆等式證明
在a>0且a≠1,N>0時
設:當log(a)(N)=t,滿足(t∈R)
則有a^t=N;
a^(log(a)(N))=a^t=N;
證明完畢
運算法則
 對數公式
對數公式①
 對數公式
對數公式②
 對數公式
對數公式③
(M,N∈R)
 對數公式
對數公式 對數公式
對數公式如果 ,則m為數a的自然對數,即 ,e=2.718281828…為自然對數
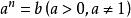 對數公式
對數公式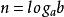 對數公式
對數公式的底,其為無限不循環小數。定義: 若 則
基本性質:
 對數公式
對數公式1、
 對數公式
對數公式2、
 對數公式
對數公式3、
 對數公式
對數公式4、
 對數公式
對數公式5、
推導:
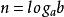 對數公式
對數公式 對數公式
對數公式 對數公式
對數公式1、因為 ,代入則 ,即 。
2、MN=M×N
由基本性質1(換掉M和N)
 對數公式
對數公式由指數的性質
 對數公式
對數公式又因為指數函式是單調函式,所以
 對數公式
對數公式3、與(2)類似處理 M/N=M÷N
由基本性質1(換掉M和N)
 對數公式
對數公式由指數的性質
 對數公式
對數公式又因為指數函式是單調函式,所以
 對數公式
對數公式4、與(2)類似處理
由基本性質1(換掉M)
 對數公式
對數公式由指數的性質
 對數公式
對數公式又因為指數函式是單調函式,所以
 對數公式
對數公式或
 對數基本性質4推導過程
對數基本性質4推導過程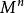 對數公式
對數公式由基本性質2(展開 ,如圖所示)
基本性質4推廣
 對數公式
對數公式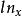 對數公式
對數公式 對數公式
對數公式推導如下: 由換底公式(見下面)[ 是 ,e稱作自然對數的底]
 對數公式
對數公式 對數公式
對數公式換底公式的推導: 設 則
 對數公式
對數公式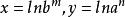 對數公式
對數公式其中
 對數公式
對數公式得:
 對數公式
對數公式由基本性質4可得
 對數公式
對數公式再由換底公式
換底公式
設b=a^m,a=c^n,則b=(c^n)^m=c^(mn)………………………………①
對①取以a為底的對數,有:log(a)(b)=m……………………………..②
對①取以c為底的對數,有:log(c)(b)=mn……………………………③
 對數公式
對數公式③/②,得:log(c)(b)/log(a)(b)=n=log(c)(a)∴log(a)(b)=log(c)(b)/log(c)(a)
註:log(a)(b)表示以a為底b的對數。
換底公式拓展:
以e為底數和以a為底數的公式代換:
logae=1/(lna)
推導公式
log(1/a)(1/b)=log(a^-1)(b^-1)=-1logab/-1=loga(b)
loga(b)*logb(a)=1
loge(x)=ln(x)
lg(x)=log10(x)
求導數
(xlogax)'=logax+1/lna
其中,logax中的a為底數,x為真數;
(logax)'=1/xlna
特殊的即a=e時有
(logex)'=(lnx)'=1/x

