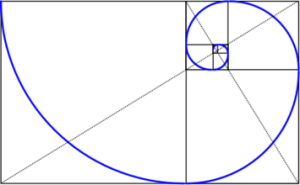
定理
等角螺線的臂的距離以幾何級數遞增。
設 L 為穿過原點的任意直線,則 L 與等角螺線的相交的角A永遠相等(故其名),而此值為 arccot(b)。
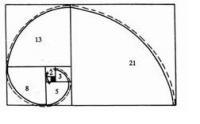 等角螺線
等角螺線 tanA=ρ/d(ρ)=ke^(bθ)/bke^(bθ)=1/b,推出:b=cot(A),推出:角A=arccot(b)。設 C 為以原點為圓心的任意圓,則 C 與等角螺線的相交的角永遠相等,而此值為 arctan(b),名為「傾斜度」
等角螺線是自我相似的;這即是說,等角螺線經放大後可與原圖完全相同。
等角螺線的漸屈線和垂足線都是等角螺線。
從原點到等角螺線的任意點上的長度有限,但由那點出發沿等角螺線走到原點卻需繞原點轉無限次。這是由 Torricelli 發現的。(由於指數函式的取值範圍為負無窮到正無窮,x=0是漸近線,因此永遠不會到達原點0,無法從原點出發,上述有誤)
建造等角螺線
在複平面上定義一個複數 z = a + bi,其中 a, b ≠ 0,那么連起 z、z²、z³…… 的曲線就是一條等角螺線。
若 L 是複平面中的一條直線且不平行於實數或虛數軸,那么指數函式 ez 會將這些直線映像到以 0 為中心的等角螺線。
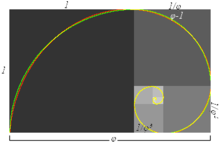 等角螺線
等角螺線 使用黃金長方形:
自然現象
鸚鵡螺的貝殼像等角螺線
菊的種子排列成等角螺線
鷹以等角螺線的方式接近它們的獵物
昆蟲以等角螺線的方式接近光源
蜘蛛網的構造與等角螺線相似
鏇渦星系的鏇臂差不多是等角螺線。銀河系的四大鏇臂的傾斜度約為 12°。
低氣壓(熱帶氣鏇、溫帶氣鏇等)的外觀像等角螺線
歷史
等角螺線是由笛卡兒在1638年發現的。雅各布.伯努利後來重新研究之。他發現了等角螺線的許多特性,如等角螺線經過各種適當的變換之後仍是等角螺線。他十分驚嘆和欣賞這曲線的特性,故要求死後將之刻在自己的墓碑上,並附詞「縱使改變,依然故我」(eadem mutata resurgo)。可惜雕刻師誤將阿基米德螺線刻了上去。
等角螺線又稱為對數螺線。