概述
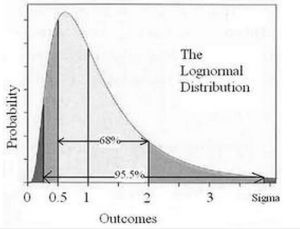
在分析測試中,特別是在衡量分析中,在不少情況下,測定值不遵循常態分配,而是遵循對數常態分配。基本定義
在機率論與統計學中,對數常態分配是對數為常態分配的任意隨機變數的機率分布。如果X是服從常態分配的隨機變數,則exp(X)服從對數常態分配;同樣,如果Y服從對數常態分配,則ln(Y)服從常態分配。如果一個變數可以看作是許多很小獨立因子的乘積,則這個變數可以看作是對數常態分配。一個典型的例子是股票投資的長期收益率,它可以看作是每天收益率的乘積。
設ξ服從對數常態分配,其密度函式為:
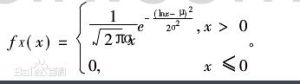 圖示
圖示"對數常態分配"在工具書中的解釋
1、一些正偏態資料的變數值,通過對數轉換後,由偏態分布轉為常態分配。某些正偏態資料,如血鉛含量、某些傳染病的潛伏期等,經對數變換後可符合常態分配。
圖片
主要學者
王玲玲 王蓉華 費鶴 良成 邦文陳舜華何基報 陶然 李 斌 張志華
陳文華
相關關係
對數常態分配、幾何平均數與幾何標準差是相互關聯的。在這種情況下,幾何平均值等於exp(μ),幾何
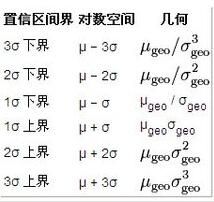
平均差等於exp(σ)。
如果採樣數據來自於對數常態分配,則幾何平均值與幾何標準差可以用於估計置信區間,就像用算術平均數與標準差估計常態分配的置信區間一樣。