對數曲線

如果aᵇ=n，那么logn=b。其中，a叫做“底數”，n叫做“真數”，b叫做“以a為底的n的對數”。logn函式叫做對數函式。對數函式中n的定義域是n>0，零和負數沒有對數；a的定義域是a>0且a≠1。其圖像為對數曲線。

定義

一般地，函式y=logx（a>0，且a≠1）叫做對數函式，也就是說以冪（真數）為自變數，指數為因變數，底數為常量的函式，叫對數函式。對數函式的 圖像 為對數曲線。

圖像性質

值域：實數集R，顯然對數函式無界；

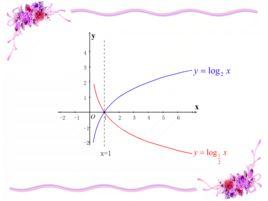
定點：對數函式的函式圖像恆過定點（1，0）；

單調性：a>1時，在定義域上為單調增函式；0<a<1時，在定義域上為單調減函式；

奇偶性：非奇非偶函式

周期性：不是周期函式

對稱性：無

最值：無

零點：x=1

注意：負數和0沒有對數。

兩句經典話：底真同對數正,底真異對數負。解釋如下：

也就是說：若y=logb （其中a>0,a≠1，b>0）

當0<a<1, 0<b<1時，y=logb>0;

當a>1, b>1時，y=logb>0;

當0<a<1, b>1時，y=logb<0;

當a>1, 0<b<1時，y=logb<0。

與其他函式與反函式之間圖象關係相同,對數函式和指數函式的圖象關於直線y=x對稱.