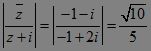基本釋意
在計算中常用到的是：i^2 = -1 ，即虛數單位的平方為負一。在複數a+bi中，a稱為複數的實部，b稱為複數的虛部，i稱為虛數單位。當虛部等於零時，這個複數就是實數；當虛部不等於零時，這個複數稱為虛數，虛數的實部a如果等於零，且虛部b不等於零，則稱為純虛數。由上可知，複數集包含了實數集，因而是實數集的擴張。
定義
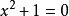虛數單位虛數單位i定義為二次方程式
的兩個解中的一個解。這方程式又可等價表達為
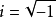虛數單位所以虛數單位同樣可以表示為：
由於實數的平方絕不可能是負數，我們假設有這么一個數目解答，給它設定一個符號i。很重要的一點是,i是一個良定義的數學構造。
性質
基本性質
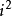虛數單位實數運算可以延伸至虛數與複數。當計算一個表達式時，我們只需要假設i是一個未知數，然後依照i的定義，替代任何
的出現為-1。的更高整數冪數也可以替代為-i，1或i，
一般地，有以下的公式：
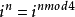虛數單位其中mod 4表示被4除的餘數。
i與-i
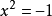虛數單位方程
有兩個不同的解，它們都是有效的，且互為共軛複數。更加確切地，一旦固定了方程的一個解i，那么−i（不等於i）也是一個解，由於這個方程是唯一的定義，因此這個定義表面上有歧義。然而，只要把其中一個解選定，並固定為i，那么實際上是沒有歧義的。這是因為，雖然−i和i在數量上不是相等的（它們是一對共軛虛數），但是i和−i之間沒有質量上的區別（−1和+1就不是這樣的）。如果所有的數學書和出版物都把虛數或複數中的+i換成−i，而把−i換成−(−i) = +i，那么所有的事實和定理都依然是正確的。
正當使用
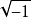虛數單位虛數單位有時記為
。但是，使用這種記法時需要非常謹慎，這是因為有些在實數範圍內成立的公式在複數範圍內並不成立。
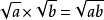虛數單位公式
僅對於非負的實數和才成立。
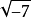虛數單位為了避免這種錯誤，儘量不要用平方根來表示虛數。例如我們不應使用
，而應使用
。
i的運算
許多實數的運算都可以推廣到，例如平方根、冪、對數和三角函式。
平方根
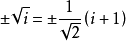虛數單位以i為底的對數
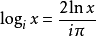虛數單位餘弦
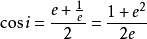虛數單位正弦
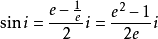虛數單位程式語言
大部分的程式語言都不提供虛數單位，且平方根函式(大多為sqrt()或Math.Sqrt())的引數不可以是負數，因此，必須自行建立類別後方可使用。
在Matlab，虛數單位的表示方法為i或j，但i和j在for循環可以有其他用途。
在Maple，必須啟用虛數功能，並選擇用i還是j表示虛數單位。
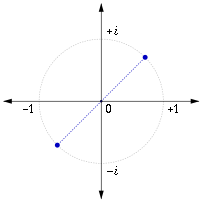虛數單位在複平面位置