概述
 子博弈精煉納什均衡
子博弈精煉納什均衡澤爾騰則在60年代中期將納什均衡概念引入動態分析。在1965年發表《需求減少條件下寡頭壟斷模型的對策論描述》一文,提出了“子博弈精煉納什均衡”的概念,又稱“子對策完
美納什均衡”。這一研究對納什均衡進行了第一次改進,選擇了更具說服力的均衡點。海薩尼在60年代末把不完全信息引入博弈分析。
將納什均衡中包含的不可置信的威脅策略剔除出去。它要求參與者的決策在任何時點上都是最優的,決策者要“隨機應變”,“向前看”,而不是固守舊略。
由於剔除了不可置信的威脅,在許多情況下,精煉納什均衡也就縮小了納什均衡的個數。這一點對預測分析是非常有意義的。
用動態博弈理論來討論實際究竟發生哪個納什均衡。
給定“歷史”,每一個行動選擇開始至博弈結束構成了一個博弈,稱為“子博弈”。
只有當參與人的策略在每一個子博弈中都構成納什均衡叫做精煉納什均衡。或者說,組成精煉納什均衡的策略必須在每一個子博弈中都是最優的。
定義
子博弈:一個擴展式表示博弈的子博弈G是由一個單結信息集x開始的與所有該決策結的後續結(包括終點結)組成的能自成一個博弈的原博弈的一部分。
對於擴展式博弈的策略組合S*=(S1*,…,Si*,…,Sn*) ,如果它是原博弈的納什均衡;它在每一個子博弈上也都構成納什均衡,則它是一個子博弈精煉納什均衡。
博弈論專家常常使用“序貫理性”(Sequential rationality):指不論過去發生了什麼,參與人應該在博弈的每個時點上最最佳化自己的策略。子博弈精煉納什均衡所要求的正是參與人應該是序慣理性的。對於有限完全信息博弈,逆向歸納法是求解子博弈精煉納什均衡的最簡便的方法。因為有限完美信息博弈的每一個決策結都開始一個子博弈。求解方法:最後一個結點上的子博弈(納什均衡)→倒數第二個(納什均衡) → ······ → 初始結點上的子博弈(納什均衡)。
動態博弈
動態是世間萬物的基本特徵。完全信息靜態博弈只是一種獨特的理想狀態。在現實中,當後一個參與人行動時,自然會根據前者的選擇而調整自己的選擇,而前者也會理性地預期到這一點,所以不可能不考慮自己的選擇對他人的影響。1965年,澤爾騰通過對動態博弈的分析,提出了“子博弈精煉納什均衡”的概念,它要求任何參與人在任何時間、地點的決策都是最優的,決策者應該隨機應變,而不是固守前謀。這就推導出子博弈的概念。當參與人的戰略在每一個子博弈中都構成納什均衡時,則形成“子博弈精煉納什均衡”。也就是說,組成“子博弈精煉納什均衡”的戰略必須在每一個子博弈中都是最優的。
意義
子博弈精煉納什均衡用於區分動態博弈中的"合理納什均衡"與"不合理納什均衡",將納什均衡中包含有不可置信威脅策略的均衡剔除出去,就是說,使最後的均衡中不再包含有不可置信威脅策略的存在。
逆向求解
逆向歸納法(Backward Induction)是求解子博弈精煉納什均衡的最簡便方法。在求解子博弈精煉納什均衡時,從最後一個子博弈開始逆推上去,這就是逆向歸納法。所以逆向歸納法就是從動態博弈的最後一個階段或最後一個子博弈開始,逐步向前倒推以求解動態博弈均衡的方法。
用逆向歸納法求解子博弈精煉納什均衡;承諾行動與子博弈精煉納什均衡;逆向歸納法與子博弈精煉均衡存在的問題。
套用舉例
 子博弈精煉納什均衡
子博弈精煉納什均衡在表1描述的博弈模型中,每一次微觀主體間的博弈均可看作一個子博弈。子博弈精煉納什均衡包含兩層含義:
(1)它是原博弈的納什均衡;
(2)它在每一個子博弈上給出納什均衡。
子博弈精煉納什均衡就是要剔除那些只在特定情況下是合理的,而在其他情況下並不合理的行動規則。
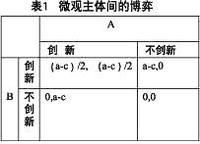
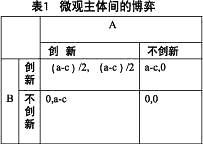
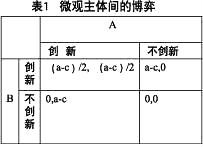
表1微觀主體間的博弈
子博弈精煉納什均衡
在表1中,a代表只有一個微觀主體創新時所帶來的收益,c代表該微觀主體創新所需付出的成本。當只有一個微觀主體進行創新時將會獲得創新帶來的全部收益(a-c),而當兩個主體同時創新時,收益將會減半(a-c)/2。一般情況下“a-c>0”,則很明顯在這個博弈過程中,(創新,創新)是一個納什均衡,更嚴格地說,是一個嚴格優勢策略均衡。依此類推,可以得出,在每一次新的金融規制後,(創新,創新)這個策略都將是至下次新規制出現前的子博弈的納什均衡。因此,在利潤的驅動下,微觀主體都會選擇創新這樣一個策略。
舉例的進一步分析
在市場進入博弈中,在給定企業B已經進入的情況下,在位者的“鬥爭”,“高價”策略已不再是最優的,這種“鬥爭”是不可置信的威脅,因為鬥爭的結果是沒有利潤;而合作會帶來50單位利潤。所以,(進入,高價)不是一個精煉納什均衡。剔除這個均衡,可以證明,(進入,低價)是唯一的子博弈精煉納什均衡。
在動態博弈中,參與人的行動有先後順序,後行動的參與人在自己行動之前就可以觀察到先行動者(參與人)的行為,並在此基礎上選擇相應的策略。而且,由於先行動者擁有後行動者可能選擇策略的完全信息,因而先行動者在選擇自己的策略時,就可以預先考慮自己的選擇對後行動者選擇的影響,並採取相應的對策。
利用房地產開發的例子,討論子博弈精煉納什均衡。表2給出了靜態條件下雙方參與人的收益情況。
表2房地產開發博弈(靜態)的收收益矩陣
子博弈精煉納什均衡
從表2可以知道,該博弈有兩個納什均衡,即(A開發,B不開發)和(A不開發,B開發),我們無法確定是開發商A選擇開發,開發商B選擇不開發,還是恰恰相反的結果。
現在,我們討論動態博弈。假定房地產開發商A是先行動者。在行動之前,開發商A對對手開發商B的策略進行了預測。在行動開始之前的A看來,如果不計得失,B有四種策略可供選擇:
策略一:無論A是否選擇開發,B選擇開發。
策略二:若A選擇開發,B也選擇開發;若A選擇不開發,B也選擇不開發。
策略三:若A選擇開發,B就選擇不開發;若A選擇不開發,B就選擇開發。
策略四:無論A是否選擇開發,B都選擇不開發。
在表2的基礎上,結合A先行動,B可能選擇的四種策略,不難得出表3。
表3先行動者A對B預測結果的收益矩陣
子博弈精煉納什均衡
由表3可以看出,在開發商A先行動的情況下,開發商B可供選擇的策略中,策略一隻包括了上述兩個納什均衡中的後一種均衡,即(A不開發,B開發),而沒有包括前一種納什均衡,即(A開發,B不開發);策略二上述兩種納什均衡都沒有包括;策略四隻包括了上述兩種納什均衡中的前一種均衡,即(A開發,B不開發),而未包括後一種納什均衡,即(A不開發,B開發);只有策略三既包括了上述兩種納什均衡中的前一種均衡,又包括了後一種均衡。也就是說,如果B選擇策略三,那么,無論A作出什麼選擇,B的回應都能達到納什均衡。反過來,在給定B會選擇策略三來回應A的選擇的前提下,開發是A的占優選擇。因此,A一定會選擇開發
盤點各種博弈策略
| 博弈論聽上去很深奧,其實每時每刻就發生在我們的身邊,有時博弈論可以成為幫助我們在一些重大人生決策時提供幫助 |