定義
在一個圓中，圓心到該圓的任一弦的距離，叫做這一弦的弦心距。
在同圓或等圓中，弦相等，弦心距也相等；反之，弦心距相等，弦也相等。
在同圓或等圓中，對於兩條不相等的弦，它們的弦心距也不等，大弦的弦心距反較小。
相關性質
圓心角、弧、弦、弦心距的性質
(1)在同圓或等圓內，如果圓心角相等，那么它們所對的弧相等，所對的弦相等，所對弦上的弦心距相等(逆命題也成立)。
(2)在同圓或等圓內，如果圓心角不等，那么圓心角大的所對的弧大，所對的弦大，所對弦上的弦心距小(逆命題也成立) 。
直徑、弦、弧的性質
(1)在圓內，如果直徑垂直弦，那么這直徑平分這弦，平分這弦所對的弦。
(2)在圓內，如果直徑平分弦(這弦本身不是直徑)，那么這直徑垂直這弦，並平分這弦所對的弧。
(3)在圓內，如果直徑平分弧，那么這直徑垂直平分這弧所對的弦。
(4)在圓內，弦的垂直平分線通過圓心。
(5)在圓內，二平行弦所夾的弧相等 。
弦心距的計算
遇到求弦長a，弦心距d，半徑r及弓形高h的問題，經常建立以半徑、半弦、弦心距為邊的直角三角形，利用勾股定理解題 。
圖1由a，d，r，h中任意兩個可求其他兩個，如圖1。
弦心距(1)若已知r、d，則
弦心距(2)若已知r、h，則
弦心距(3)若已知r、a，則
弦心距(4)若已知d、h，則
弦心距(5)若已知a、d，則
弦心距(6)若已知a、h，則
有關弦長、弦心距的計算問題往往需要作垂直於弦的直徑(半徑或弦心距)，利用垂徑定理平分弦的結論以及半徑、弦心距和弦的一半組成的直角三角形達到求解的目的，也可用相交弦定理的推論解題 。
【例1】 本市新建的滴水湖是圓形人工湖，為測量該湖的半徑，小傑和小麗沿湖邊選取A，B，C三根木柱，使得A，B之間的距離與A，C之間的距離相等，並測得BC長為240 m，A到BC的距離為5m，如圖2所示，請你幫他們求出滴水湖的半徑。
圖2解 析 本題涉及垂徑定理及其推論知識，得OA⊥BC，再利用勾股定理求解。
解：連線OA交BC於D，連線OB。
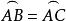弦心距因為AB= AC，所以 ，
所以OA⊥BC，且BD=DC=1/2BC= 120，
由題意知DA=5，
在Rt△BDO中，OB²=OD²+BD²，
弦心距設OB= m，則
弦心距所以x=1442.5.
答：滴水湖的半徑為1442.5 m 。
