完全四邊形

幾何中的完全四邊形

完全四邊形的定義

完全四邊形,由四條直線或球面上四條大圓的弧組成，其中每一條直線或弧都與其餘的直線或弧相交於三點（即沒有三線共點）所構成的圖形。或者我們把兩兩相交,且沒有三線共點的四條直線及它們的六個交點所構成的圖形,叫做完全四邊形。
如圖所示，在完全四邊形中ADCFBE，有四個三角形：ΔACE、ΔABD、ΔCDF、ΔBEF，有凸四邊形ADFE，凹四邊形ACFB，折四邊形CDEB，六個點A、B、C、D、E、F，三條對角線AF、DE、BC。

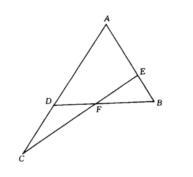
完全四邊形的性質

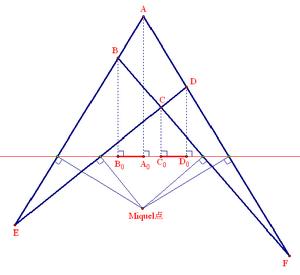
1。完全四邊形中四個三角形的外接圓共點，此點稱為密克點。
2。完全四邊形中四個三角形的垂心共線，稱為垂心線。
3。完全四邊形的一條對角線被其餘兩條對角線調和分割。
4。過完全四邊形的密克點作四個三角形的西姆松線，所得四線重合，稱為完全四邊形的西姆松線。
5。完全四邊形的西姆松線與垂心線平行。
6。完全四邊形的任一組“對節”在西姆松線線（或垂心線，因為它們平行）上的射影，其長度總保持相等。
7。完全四邊形三條對角線的中點三點共線，這條直線與完全四邊形的西姆松線、垂心線垂直，這條線稱為牛頓線。
8。梅涅勞斯定理。
9。完全四邊形的三條對角線為直徑的圓共軸，且完全四邊形的四個三角形的垂心在這條軸上，此線稱為完全四邊形的垂足線。垂足線與牛頓線垂直。
10。完全四邊形的四個三角形的外接圓圓心共圓，這四個圓心每三個構成的三角形的垂心分辨在構成完全四邊形的四條直線上，且這四個垂心為頂點構成的四邊形與四個圓心為頂點構成的四邊形全等。
11。在完全四邊形ABCDEF中，點G是對角線AD所在直線上抑異於點A的任意一點，則
cot∠AGC+cot∠AGF=cot∠AGB+COT∠AGE

完全四邊形的深入研究

在《近代歐氏幾何學》§195中有一條關於Simson線的比較隱蔽的性質：
“三角形任一邊在一點的西摩松線上的射影，等於這點到其他兩邊的垂線的垂足之間的距離。”
同樣，在梁紹鴻《初等數學複習及研究（平面幾何）》中也有這一命題：
“圓上一點對於內接三角形的西摩松線夾於該三角形任兩邊（所在直線）間的線段，等於第三邊在該西摩松線上的射影。”（複習題三第44題）
其實它揭示了完全四邊形的一個深刻屬性：
命題：完全四邊形的任一組“對節”在Simson線（或垂心線，因為它們平行）上的射影，其長度總保持相等！

如右下圖中，紅線是完全四邊形ABCD的Simson線（Miquel點在完全四邊形的四邊上射影所共之線），對節AB、CD在Simson線上的射影分別為A0B0、C0D0。則總成立A0B0=C0D0。

如左下圖，如果把完全四邊形還原為Apollonius研究過的拋物線的切線，那么這個命題還相當於拋物線切線的如下性質：
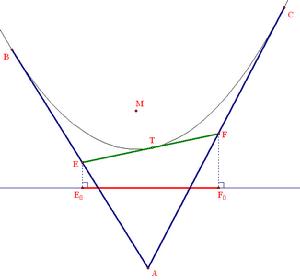
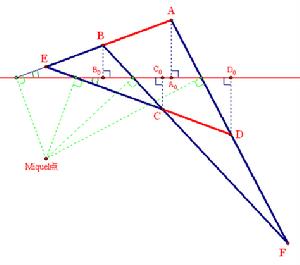
拋物線的動切線夾在兩條定切線AB、AC之間的線段EF，在準線上的射影E0F0保持定長！

其實，2003年女子競賽中的平幾題也有這一背景：
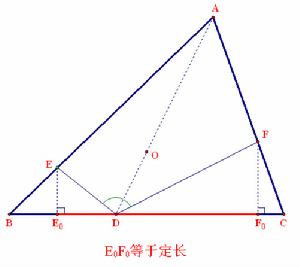
如右圖，在△ABC中，外接圓半徑AO的延長線交對邊於D，過D任作一角EDF（E、F分別在AB、AC上）等於180°－∠A，則E、F在底邊BC上的射影E0、F0間的距離保持不變（不隨∠EDF的轉動而變化）。
題中，直線AB、AC及動直線EF任意兩個位置形成一個完全四邊形，D相當於其Miquel點，而BC邊的方向恰平行於準線（或Simson線）。

如左圖，在閔飛一題的討論中，我們將問題歸結為完全四邊形某一組對節的相等。但是兩條線段的長度既要相等，其射影（在同一條直線上的）也必需相等，這究竟怎么回事？
注意：射影長等於線段的長度乘以傾斜角的餘弦。因此只有如下兩種可能：一是這組對節既平行又相等，即形成一個平行四邊形——這是一種退化的情形（因為這時完全四邊形的特徵全消失了）；
二是這組對節位於Simson線的異側，其實這時傾斜角不是相等，而是相反：

記起了一個常見習題：
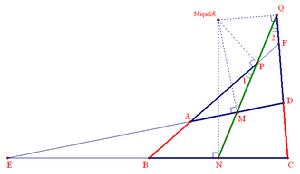
“如右圖，在四邊形ABCD中，AB=CD，M、N分別是對邊AD、BC的中點，直線MN分別與BA、CD的延長線交於P、Q點。求證：∠APM=∠DQM。”
現在可以看出本題的另一重背景來了：直線MN正是完全四邊形ABCD的Simson線！難怪它和這組對節所在的直線交角必須相等，呵呵。

圖論中的完全四邊形

圖論中有個完全圖的概念，代表含有n個頂點而且每兩個頂點之間恰好有一條邊的無向圖。所以n個頂點的完全圖含有n(n-1)/2條邊。通常我們記n個頂點的完全圖為Kn,而其中K4稱為完全四邊形。