圓內接正五邊形
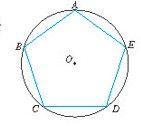 圓內接正五邊形
圓內接正五邊形圓內接正五邊形的定義與性質:
| 定義 | 內接於圓的正五邊形是圓內接正五邊形 |
| 性質 | 圓內接正五邊形五條邊長度相等。(即圓的五條弦長度相等) |
| 圓內接正五邊形的五個內角相等,都是108° | |
| 圓內接正五邊形的五條邊在圓內所對的五條優弧長度相等 | |
| 圓內接正五邊形的五條邊在圓內所對的五條優弧的弧度數相等 | |
圓的五等分及圓內接五邊形作法
 圓內接五邊形
圓內接五邊形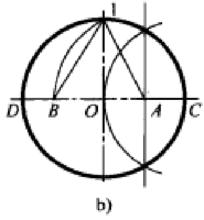 圓內接五邊形
圓內接五邊形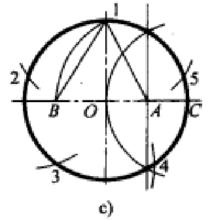 圓內接五邊形
圓內接五邊形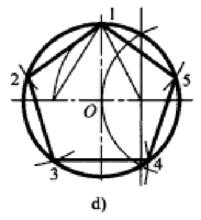 圓內接五邊形
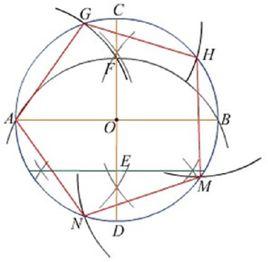
圓內接五邊形作圖步驟 :
(1)畫一互相垂直的中心線並作圓,確定圓心為O。
(2)找OC的中點A,也就是作OC的垂直平分線來確定點A。以點C為圓心,以CO為半徑畫弧和圓交於兩點,用直線連線兩交點,則該直線與OC的交點A即OC的中點。
(3)以A為圓心,以A1為半徑畫弧,交OD於B點。
(4)以1B為半徑,用畫規或圓規在圓上分別畫弧取1、2、3、4、5點,即完成圓的五等分。 ’
(5)分別連線12、23、34、45、51,即完成圓內接五邊形。
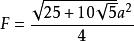 圓內接五邊形
圓內接五邊形1991年,王振和陳計老師用Galois理論證實了一個命題,即:圓內接五邊形的面積一般不能用邊長的根式表示.但是,對於某些邊長出現重複的圓內接五邊形,仍能給出其根式形式或三角形式的面積公式.比如正五邊形,設其邊長為口,則其面積 .除此之外,其他特殊類型的圓內接五邊形及其面積公式似乎尚未被研究發表.這裡列出兩類邊長出現重複的圓內接五邊形——“鑽石五邊形”和“對稱五邊形”,並分別給出二者的面積公式.
鑽石五邊形
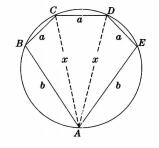
定義:稱邊長依次為b,a,a,a,b的圓內接五邊形為“鑽石五邊形”(如圖)
 圓內接五邊形
圓內接五邊形面積F=
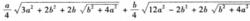 圓內接五邊形
圓內接五邊形對稱五邊形
定義 稱邊長依次為b,a,c,a,b(c<2a+2b)的圓內接五邊形為“對稱五邊形 ”(如圖).
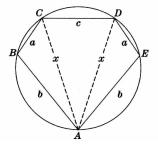 圓內接五邊形
圓內接五邊形面積F=
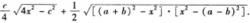 圓內接五邊形
圓內接五邊形“鑽石五邊形”和“對稱五邊形”兩類圓內接五邊形同構形的面積公式
定義:稱兩個邊長相同、邊的排列次序不同的圓內接n邊形互為同構形.
我們要給出的結論是:“鑽石五邊形”同構形與“鑽石五邊形”有相同的面積公式;“對稱五邊形”同構形
與“對稱五邊形”也有相同的面積公式.
 圓內接五邊形
圓內接五邊形事實上,我們可以得到更廣的結論:同構的圓內接n邊形面積相等.證此結論需藉助如下引理(該引理是
判定三角形全等的“邊邊邊”定理的推廣.
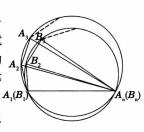
引理:兩個對應邊長相等的圓內接凸n邊形全等.
證明 以P表示凸n邊形A1A2…An,Q表示凸n邊形B1B2…Bn,令R和r分別為P和Q的外接圓半徑.
如果P和Q的外接圓半徑不相等,設R>r.不妨設A1A2和B1B2分別為P和Q的最長邊.由於外接圓半徑愈大,等長的弦所張成的圓心角(及跟圓心同側的圓周角)愈小,所以對於i=2,3,…,n一1,由於R>r,故∠Ai-1AnAi<∠Bi—1BnBi,於是∠A1AnAi=∠A1AnA2+∠A2AnA3+......+∠Ai-1AnAi<∠B1BnB2+∠B2BnB3+∠Bi-1BnBi=∠B1BnBi同理∠AnA1Ai<∠BnB1Bi.如圖,把A1An移至跟B1Bn重合.考慮ΔA1AnAi和ΔB1BnBi(i=2,3,…,n-1),由上可知,ΔA1AnAi被ΔB1BnBi覆蓋,即頂點Ai是ΔB1BnBi的內點,當然也就是凸n邊形Q的內點.因此P完全被Q所覆蓋,且P不與Q重合.根據凸多邊形的周界性質,凸n邊形P的周長嚴格小於凸n邊形Q的周長,這與兩者對應邊長相等的已知條件矛盾.所以P和Q的外接圓半徑相等,並因此P和Q全等.引理證畢.證明上面提及的“更廣的結論”.記A和B是兩個同構的圓內接n邊形,以A的外接圓圓心O為頂點,以A的各邊為底邊可形成n個等腰三角形,在圓O中將這n個等腰三角形調換位置按頂點在O處重新拼接,使得各底邊與B中各邊的排列次序相同.記這個由A生成,與B中各邊排列次序相同的圓內接n邊形為C,由於這種變換是等積變換,所以C和A面積相等.又由於C和B是兩個對應邊長相等的圓內接凸n邊形,根據引理,二者全等,所以面積相等.於是A和B的面積相等 .