定義
定義1
半平面是立體幾何的基本概念之一。一條直線將平面分為兩部分,其中的每一部分均稱為 半平面。例如,若a是平面α上的一條直線,則將α上不屬於a的點按以下性質分為兩個集合:連結同一個集合的兩點的線段不與a相交,連結不同集合的兩點的線段必與a相交。這兩個集合都稱為半平面,直線a稱為這兩個半平面的邊界或邊緣,包含邊界的半平面稱為閉半平面,不包含邊界的半平面稱為開半平面。
定義2
 半平面
半平面 半平面
半平面 半平面
半平面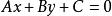 半平面
半平面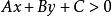 半平面
半平面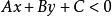 半平面
半平面歐氏平面被平面上一直線分割成兩部分,其中每一部分都稱做 半平面,直線可以屬於兩半平面中的任一個,若直線的方程為(A,B不同時為零),且它不屬於兩半平面中的任何一個,則該直線所確定的兩半平面中一個上的點都滿足,而另半平面上的點都滿足。
定義3
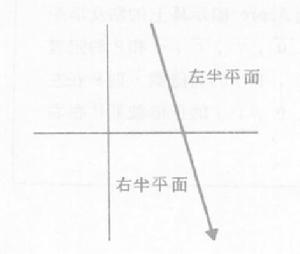
所謂半平面,就是指一條直線一側的部分。若規定直線的正方向.則沿正方向看去,左側的部分稱為 左半平面,右側的部分稱為 右半平面。直線上的點屬於哪個半平面,需根據實際問題,具體判斷。
定義4
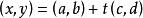 半平面
半平面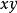 半平面
半平面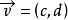 半平面
半平面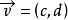 半平面
半平面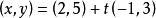 半平面
半平面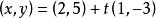 半平面
半平面直線將平面分割成兩個半平面。若對著向量的方向時,在左邊的半平面稱為 左半平面,在右邊的半平面稱為 右半平面。請注意左右半平面的定義是由向量的方向所決定。例如:直線所分割的平面如圖1,直線(同樣的直線但方向相反)分割的平面如圖2。
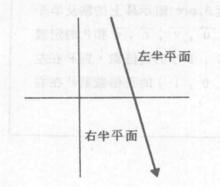 圖1
圖1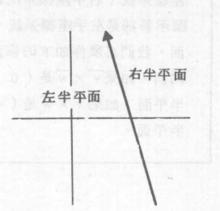 圖2
圖2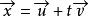 半平面
半平面有時討論半平面,是要決定哪個半平面包含所給定的點,對於由直線分割的平面,它的左半平面與右半平面如3所示。
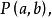 半平面
半平面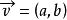 半平面
半平面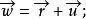 半平面
半平面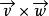 半平面
半平面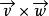 半平面
半平面要決定那個半平面包含點我們可以定義向量,如果P在左半平面,則是(0,0,1)的正倍數;如果P在右半平面,則是(0,0,1)的負倍數。
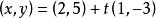 半平面
半平面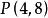 半平面
半平面考慮直線和點:
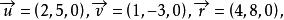 半平面
半平面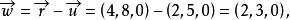 半平面
半平面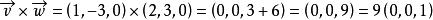 半平面
半平面是(0,0,1)的正倍數,我們可以從圖3中看出P點確實在左半平面。
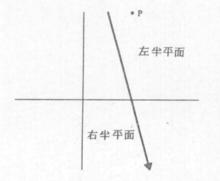 圖3
圖3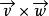 半平面
半平面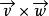 半平面
半平面注意:上面測定點位於左或右半平面的方法適用於右手坐標系統(右手坐標系統在計算時較常使用),然對於左手坐標系統,其他條件相同,如果P在左半平面,則是(0,0,1)的負倍數;如果P在右半平面,則是(0,0,1)的正倍數。
複平面的半平面
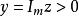 半平面
半平面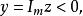 半平面
半平面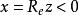 半平面
半平面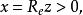 半平面
半平面對於複平面,常研究所謂上半平面和下半平面左半平面和右半平面復上半平面可以通過分式線性函式
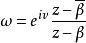 半平面
半平面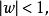 半平面
半平面 半平面
半平面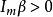 半平面
半平面保角映射為圓其中為任一複數,。