二次曲面

一般說來，直線與二次曲面相交於兩個點；如果相交於三個點以上，那么此直線全部在曲面上。這時稱此直線為曲面的母線。如果二次曲面被平行平面所截，其截線是二次曲線。二次曲面的一組具有尋常方向的平行弦中點在同一平面上。在歐氏三維空間裡坐標x,y,z之間的二次方程（係數為實數，且二次項係數不全為零）所表示的曲面。方程組的解稱為一般二次曲面F(x,y,z)=0的中心。二次曲面有如x2+y2+z2+1=0這樣的空集情況。對於鏇轉橢圓面，當α=b=с時，曲面成為以α為半徑的球面。

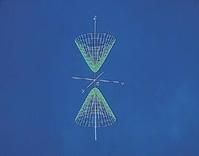
簡介

二次曲面

二次曲面

second-degree surface

在三維坐標系(x、y、z)下三元二次代數方程對應的所有圖形的統稱。

介紹

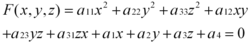二次曲面

在歐氏三維空間裡坐標x,y,z之間的二次方程（係數為實數，且二次項係數不全為零）所表示的曲面。一般說來，直線與二次曲面相交於兩個點；如果相交於三個點以上，那么此直線全部在曲面上。這時稱此直線為曲面的母線。如果二次曲面被平行平面所截，其截線是二次曲線。

二次曲面的方程為：

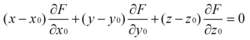奇異方向

曲面F(x,y,z)=0上適合 的點(x0,y0,z0)稱為奇異點或奇點，其他點稱為尋常點。過曲面的尋常點所作的切線構成一個平面，稱為該點的切面。通過該點且與切面垂直的直線稱為法線。F(x,y,z)=0於尋常點 (x0,y0,z0)處的切面與法線方程分別是與分類二次曲面上不在同一母線上任何兩點所聯的線段稱為弦，對於二

次曲面F(x,y,z)=0,如果一條直線的方向餘弦l,m,n，若適合右式

則此直線所對應的方向稱為曲面的奇異方向，否則稱為尋常方向。

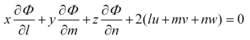徑平面方程

二次曲面的一組具有尋常方向的平行弦中點在同一平面上。這個平面稱為該方向的徑平面。此方向稱為徑平面的共軛方向。F(x,y,z)=0的以方向餘弦l,m,n為共軛方向的徑平面方程為 下式：

關於徑平面，當方向餘弦l,m,n變動時,無數多的徑平面形成一個平面族,方程是l(αx+hy+gz+u)+m(hx+by+ƒz+υ)+n(gx+ƒy+сz+w)=0。方程組的解稱為一般二次曲面F(x,y,z)=0的中心。如果中心位於二次曲面上，則稱為頂點。中心的幾何意義是：二次曲面的通過中心的任何弦都以中心為中點。

二次曲面有如x2+y2+z2+1=0這樣的空集情況。

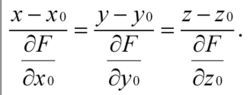二次曲面

方程形如(8)、(10)、(11)、(2)、(3)的曲面，分別稱為橢圓面，單葉雙曲面，雙葉雙曲面，橢圓柱面或橢圓柱，

雙曲柱面或雙曲柱；

對於(8)、(10)、(11)、(1)當α=b時,這些曲面是以z軸為鏇轉軸的鏇轉曲面,把它們分別稱為鏇轉橢圓面，鏇轉單葉雙曲面，鏇轉雙葉雙曲面，圓柱面或圓柱。對於鏇轉橢圓面，當α=b=с時，曲面成為以α為半徑的球面。

在方程(9)，(12)，(4)的情況，曲面分別稱為橢圓拋物面，雙曲拋物面，拋物柱面或拋物柱；對於(9)，當α=b時，曲面成為以z軸為鏇轉軸的鏇轉橢圓拋物面（見彩圖）。 二次曲面(6)的曲面是二階錐面，當a、b、c異號時,可以認為a>0,b>0,c=-1，曲面稱為實錐面，且當a=b時，曲面稱為直圓錐面。它是以z軸為鏇轉軸的鏇轉曲面；在方程(6)當a、b、c同號時,曲面變成點O，也稱為虛錐面；(2),(3)……(13)稱為這些曲面方程的標準型(標準型的α，b，с與(1)中的α，b，с不同)。

此外還有二次曲面的空集情況與另一個特殊情況，它們是虛橢圓面、虛橢圓柱面；對於(16)，曲面成為一對相交虛平面（交線為實直線）；對於(17)，曲面成為一對平行虛平面。因此共有17種情況。

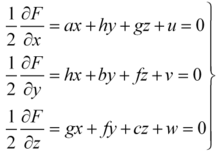方程組

這17種情況,可以根據方程組(見下式)

的係數矩陣與增廣矩陣的秩數 rank M 與 rank分類，由於rank M≤3，≤3，rank M≤rank,故知僅有五種情況(表1)。

對於曲面(8)，(11)，(10)來說，平面x=0,y=0,z=0;以及對於曲面(3)，(4)來說，平面x=0,y=0,分別稱為曲面的主平面，主平面的交線稱為主軸。對於鏇轉曲面來說，主平面及主軸的位置是不定的。標準方程中的α，b,с稱為半主軸的長度或半主軸。在單葉雙曲面或雙曲拋物面上分別存在兩族母線，同族的二母線不相交（也不平行），不同族的二母線必相交，即對於(11)，其上有以λ及μ為參數的母線族對於(4)，其上有母線族能用直線生成的曲面稱為直紋曲面，二次曲面中只有單葉雙曲面和雙曲拋物面是具有兩族母線的直紋曲面。二次柱面和二次錐面是具有一族母線的直紋曲面。而鏇轉單葉雙曲面、圓柱面和直圓錐面既是直紋曲面又是鏇轉曲面。

二次超曲面

在歐氏n維空間裡，坐標（x1，x2，…，xn）之間的二次方程 ，(18)式中αik，bi，с都是實數，且不失一般性，可設矩陣A=(αik)為對稱矩陣；A為非零矩陣所表示的點集稱為n維歐氏空間裡的二次超曲面，或簡稱二次曲面。當n=2時，它成為二次曲線。當 n=3時成為二次曲面。上述關於二次曲面的分類等理論，可以推廣到n維的情況，即可以根據n維歐氏空間的坐標變換，將方程(18)化為標準型，由於n+1階方陣 與n階方陣A二者秩數間的不同關係可以得到各種不同情況。對偶地可以定義二級超曲面，它是二級曲線與二級曲面的高維推廣。

判別法

對於二次曲面的一般式

Ax^2+By^2+Cz^2+2Dyz+2Exz+2Fxy+2Gx+2Hy+2Iz+J=0

....|A...F...E...G|...............|A...F...E|

....|F...B...D...H|...........δ=|F...B...D|...........................S=A+B+C

Δ=|E...D...C...I |...............|E...D...C|

....|G...H....I....J|......................................................稱為二次曲面的不變數。

又設

.............|A...F...G|...............|B...D...H|...............|A...E...G|

.......Δ1=|F...B...H|.........Δ2=|D...C....I|.........Δ3=|E...C....I|..........Δ0=Δ1+Δ2+Δ3

.............|G...H...J|................|H....I....J|...............|G....I....J|

δ0=|A...F| + |B...D| + |A...E|

......|F...B|....|D...C|....|E...C|..................S1=A+B............S2=B+C..............S3=A+C

δ>0	Δ=0				點
...	Δ≠0			ΔS>0	虛橢球面
...	...			ΔS<0	橢球面
δ<0	Δ>0				單葉雙曲面
...	Δ=0				二次錐面
...	Δ<0				雙葉雙曲面
δ=0	Δ<0				橢圓拋物面
...	Δ>0				雙曲拋物面
...	Δ=0	δ0>0	Δ0=0		線
...	...	...	Δ0≠0	Δ1*S1+Δ2*S2+Δ3*S3>0	虛橢圓柱面
...	...	...	...	Δ1*S1+Δ2*S2+Δ3*S3<0	橢圓柱面
...	...	δ0<0	Δ0=0		相交平面
...	...	...	Δ0≠0		雙曲柱面
...	...	δ0=0	Δ0≠0		拋物柱面
...	...	...	Δ0=0	G^2+H^2+I^2-JS>0	平行平面
...	...	...	...	G^2+H^2+I^2-JS=0	重合平面
...	...	...	...	G^2+H^2+I^2-JS<0	平行虛平面 x^2/a^2+y^2/b^2-z^2/c^2=0