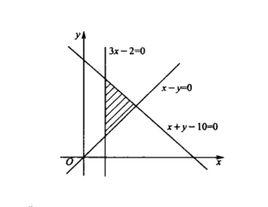
基本介紹
在平面仿射坐標系中，一直線l：Ax+By+C=0將此平面內l以外的任意兩點P(x，y)和P(x，y)為端點的線段PP所分成的比為
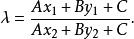直線劃分平面當Ax+By+C與Ax+By+C異號，即λ>0時，直線l與線段PP相交，即點P，P在直線l的異側；當Ax+By+C與Ax+By+C同號，即λ<0時，直線l與線段PP不相交，即點P，P在直線l的同側。可見，直線l：Ax+By+C=0將平面分為兩個半平面，其中一個半平面內的點的坐標適合不等式Ax+By+C>0，另一個半平面內的點的坐標適合不等式Ax+By+C<0。因此，如同平面上的直線可以看做二元一次方程的幾何表示一樣，半平面可以看做是二元一次不等式的幾何表示，由“同側同號，異側異號”的法則，要判別點P(x，y)在直線l：Ax+By+C=0的哪一側的具體方法可有 ：
1.若A>0，則點P在直線l的右側(x軸正向所指的一側)的充分必要條件是Ax+By+C>0；
2.若B>0，則點P在直線l的上側(y軸正向所指的一側)的充分必要條件是Ax+By+C>0；
3.若C>0，則點P與原點在直線l的同側的充分必要條件是Ax+By+C>0；
4.直線l的法向量(A，B)所指的一側的點的坐標滿足Ax+By+C>0，另一側的點的坐標滿足Ax+By+C<0；
5.若規定直線Ax+By+C=0的正方向為向量(B，-A)所指的方向，則半平面Ax+By+C>0在有向直線的左側 。
相關性質及其證明
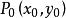直線劃分平面我們已經知道，如果點不在直線l:Ax+ By+C=0上，那么Ax+ By+C≠0.現在進一步證明以下重要結論:
把在直線l不同側的任意兩點的坐標代入二元一次式Ax + By+C，得到的數值異號；把在直線l同側的任意兩點的坐標代入二元一次式Ax+By+C，得到的數值同號 。
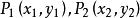直線劃分平面證明設已知兩點及直線l:Ax+ By+C=0。
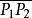直線劃分平面(1)如果經過P₁、P₂的直線與直線l相交，設交點為P,點P分所成的比為λ，則點P的坐標為
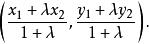直線劃分平面因為點P在直線l上，所以點P的坐標必滿足直線l的方程，即有
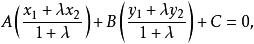直線劃分平面
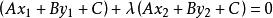直線劃分平面整理後,得，所以
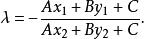直線劃分平面 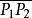直線劃分平面
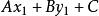直線劃分平面
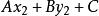直線劃分平面 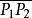直線劃分平面 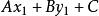直線劃分平面 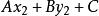直線劃分平面由此可見:當點P₁、P₂分別在直線l的兩側時，點P內分，分比λ>0，因此與異號；當點P、Pr在直線l的同側時，點P外分，分比λ<0，因此與同號。
(2)如果經過點P₁、P₂的直線與直線l平行(此時點P₁、P₂在直線l的同側)，則此二直線的斜率相等，即有
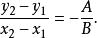直線劃分平面整理後得
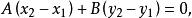直線劃分平面即
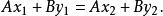直線劃分平面 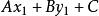直線劃分平面 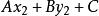直線劃分平面因此與同號。
由以上已證明的重要結論可知:
直線l:Ax+ By+C=0把坐標平面分為兩個半平面，其中一個半平面內的點的坐標滿足Ax+ By+C>0，另一個半平面內的點的坐標滿足Ax+ By+C<0。
在實際套用時，由於直線同一側的點的坐標代入Ax+By+C所得的值的符號相同，因此只要取不在直線上的一個點的坐標代入Ax+ By+C,由所得的值的符號，便可決定整個一側的點集的坐標代入Ax+By+C後所得的值的符號，下面分兩種情況討論：
(1)當C≠0時，直線不經過原點,Ax+ By+ C在原點處的值就是C，所以如果C>0，說明原點所在一側的區域Ax+ By+C>0,另一側Ax+By+C<0;如果C<0,說明原點所在一側的區域Ax+ By+C<0,另一側Ax+ By+C>0.
(2)當C=0時,直線過原點，同樣可用不在直線上一點的坐標代入Ax+ By，由所得值的符號決定區域的符號，為了方便起見，可選用點(1,0)或(0,-1)代人計算 。
