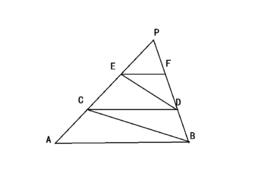
定義
兩個多邊形不僅相似，而且對應頂點的連線相交於一點，並且對應邊互相平行或位於同一直線上，像這樣的兩個圖形叫做位似圖形（homothetic figures），這個交點叫做位似中心，這時的相似比又稱為位似比。
有必要聲明，位似圖形的標準定義應是：如果兩個圖形不僅是相似圖形,且對應點連線相交於一點，對應線段相互平行，那么這樣的兩個圖形叫做位似圖形，位似圖形對應點連線的交點是位似中心。
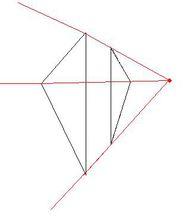和此為錯例 對應線段未相互平行錯例：對應線段未相互平行。
性質
位似圖形的任意一對對應點與位似中心在同一直線上，它們到位似中心的距離之比等於相似比。
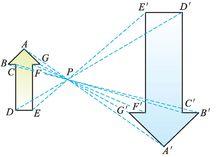位似圖形1.位似圖形對應線段的比等於相似比。
2.位似圖形的對應角都相等。
3.位似圖形對應點連線的交點是位似中心。
4.位似圖形面積的比等於相似比的平方。
5.位似圖形高、周長的比都等於相似比。
6.位似圖形對應邊互相平行或在同一直線上。
作用
利用位似可以將一個圖形任意放大或縮小。
位似中心的落點
位似圖形的中心可以在任意的一點，不過位似圖形也會隨著位似中心的位變而位變。
根據一個位似中心可以作兩個關於已知圖形一定位似比的位似圖形,這兩個圖形分布在位似中心的兩側,並且關於位似中心對稱。
作圖步驟 位似比，即位似圖形的相似比，指的是要求畫的新圖形與參照的原圖形的相似比
①首先確定位似中心，位似中心的位置可隨意選擇；
②確定原圖形的關鍵點，如四邊形有四個關鍵點，即它的四個頂點；
③確定位似比，根據位似比的取值，可以判斷是將一個圖形放大還是縮小；
④符合要求的圖形不惟一，因為所作的圖形與所確定的位似中心的位置有關，並且同一個位似中心的兩側各有一個符合要求的圖形，最好做兩個。
位似變換 把一個幾何圖形變換成與之位似的圖形,叫做位似變換。物理中的透鏡成像就是一種位似變換,位似中心為光心. 位似變換套用極為廣泛，特別是可以證明三點共線等問題.
